filmov
tv
German Federal Math Olympiad 2000 R2 P1

Показать описание
German Federal Math Olympiad 2000 R2 P1
amazing equation of Germany math olympiad
german math olympiad | 4th round | short math puzzle simply explained | MatheFIT
German Olympiad Problem
Find ONE Solution to This Equation | BMO 2000 Round 2
Can You Find Red angle ? Olympiad Question from Germany.
Ukraine - Math Olympiad Problem 2000 | Find all values of x
Difference between Men & Women World Champions 😟
Top 20 Country by International Mathematical Olympiad Gold Medal (1959-2019)
ILLEGAL Move & WIN the Game! #shorts
Comment yes for more body language videos! #selfhelp #personaldevelopment #selfimprovement
11 year old beats a Grandmaster & SMILES! #shorts
African Mathematical olympiad 2000
Pakistan education system what a beautiful environment WOW🤣🤣
A Nice and Symmetric Equation | Polish Mathematical Olympiad Second Round
When an 8 Year Old Prodigy Challenged Hikaru
How to eat Roti #SSB #SSB Preparation #Defence #Army #Best Defence Academy #OLQ
Tough times Never last 😊✌️ #delhipolice #motivation
Belarus Maths Olympiad 1995 | A simple functional equation problem
amazing Australian mathematical Olympiad number theory equation
Top 20 International Education Rankings in Mathematics; by mean score of PISA (2000~2015)
JEE: Bring ID Card & Reach center TWO hours before #jee #jee2024 #jeeexam #jeepreparation #kira...
Turkish Junior National Math Olympiad 2020 P1 - Easy technical algebra
A problem from Moscow Math Olympiad 1941
Комментарии
 0:10:30
0:10:30
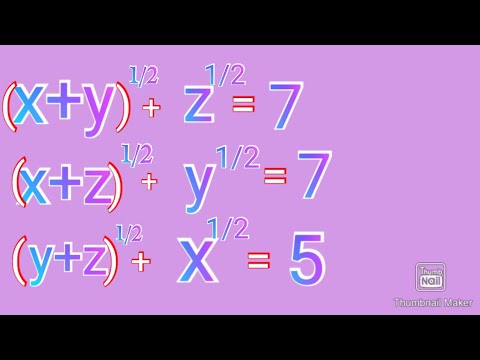 0:17:59
0:17:59
 0:07:37
0:07:37
 0:17:42
0:17:42
 0:07:49
0:07:49
 0:02:58
0:02:58
 0:08:13
0:08:13
 0:00:36
0:00:36
 0:02:21
0:02:21
 0:00:35
0:00:35
 0:00:22
0:00:22
 0:00:46
0:00:46
 0:12:09
0:12:09
 0:00:16
0:00:16
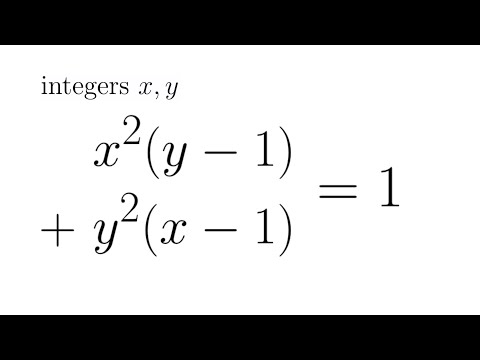 0:07:35
0:07:35
 0:05:34
0:05:34
 0:00:16
0:00:16
 0:00:22
0:00:22
 0:04:44
0:04:44
 0:10:08
0:10:08
 0:02:12
0:02:12
 0:00:22
0:00:22
 0:08:09
0:08:09
 0:03:12
0:03:12