filmov
tv
Numerical Integration: Discrete Riemann Integrals and Trapezoid Rule

Показать описание
In this video, I show how to approximate definite integrals to find the area under a curve using discrete numerical methods. In particular, I discuss approximations to the Riemann integral, including left and right rectangle rules, trapezoidal integration, and Simpson's rule based on spline interpolation. Importantly, we discuss the error of each method, compute them in Python and Matlab, and relate these techniques to other intuitive numerical schemes. All with pictures.
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Numerical integration: Discrete Riemann integrals
10:53 Trapezoidal integration
18:42 Simpson's integration rule
22:56 Python code example
26:34 Matlab code example
@eigensteve on Twitter
This video was produced at the University of Washington
%%% CHAPTERS %%%
0:00 Numerical integration: Discrete Riemann integrals
10:53 Trapezoidal integration
18:42 Simpson's integration rule
22:56 Python code example
26:34 Matlab code example
Numerical Integration: Discrete Riemann Integrals and Trapezoid Rule
Lecture -- Introduction to Numerical Integration and Discrete Integration
Numerical integration Riemann sum method
Numerical Integration is nice! #math #fy #short #calculus #mathematics #integration
How REAL Men Integrate Functions
Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
How to Find a Definite Integral using Riemann Sums and the Limit Definition: Quadratic Example
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Numerical Integration for Beginners 1 Return to Riemann Sums
Converting a Riemann Sum to a Definite Integral
Simpson's Rule & Numerical Integration
Definite integral as the limit of a Riemann sum | AP Calculus AB | Khan Academy
Trapezoidal Rule
Every Student Should See This
3 Integrals You Won't See in Calculus (And the 2 You Will)
Riemann Integration sem 4 bsc maths previous year question paper 2023 delhi university
Integration in PYTHON (Symbolic AND Numeric)
What is Integration? 3 Ways to Interpret Integrals
|Numerical Integration| What is Simpson's Rule? [Intuition]
Math 1a Spring 2021 Riemann Integral
when calculus students use trig identities too early
Riemann sum | Path way to numerical integration
Calculus 2: Approximate Integration | Midpoint, Trapezoidal & Simpson’s Rule | Math with Profess...
Комментарии
 0:29:43
0:29:43
 0:06:35
0:06:35
 0:10:26
0:10:26
 0:00:10
0:00:10
 0:00:35
0:00:35
 0:04:52
0:04:52
 0:13:18
0:13:18
 0:00:09
0:00:09
 0:00:38
0:00:38
 0:02:31
0:02:31
 0:03:13
0:03:13
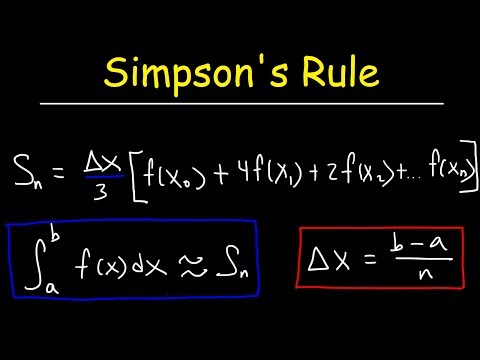 0:12:11
0:12:11
 0:04:26
0:04:26
 0:12:10
0:12:10
 0:00:58
0:00:58
 0:12:05
0:12:05
 0:00:11
0:00:11
 0:15:20
0:15:20
 0:10:55
0:10:55
 0:02:51
0:02:51
 0:12:28
0:12:28
 0:00:43
0:00:43
 0:15:33
0:15:33
 0:55:59
0:55:59