det AB = det A det B

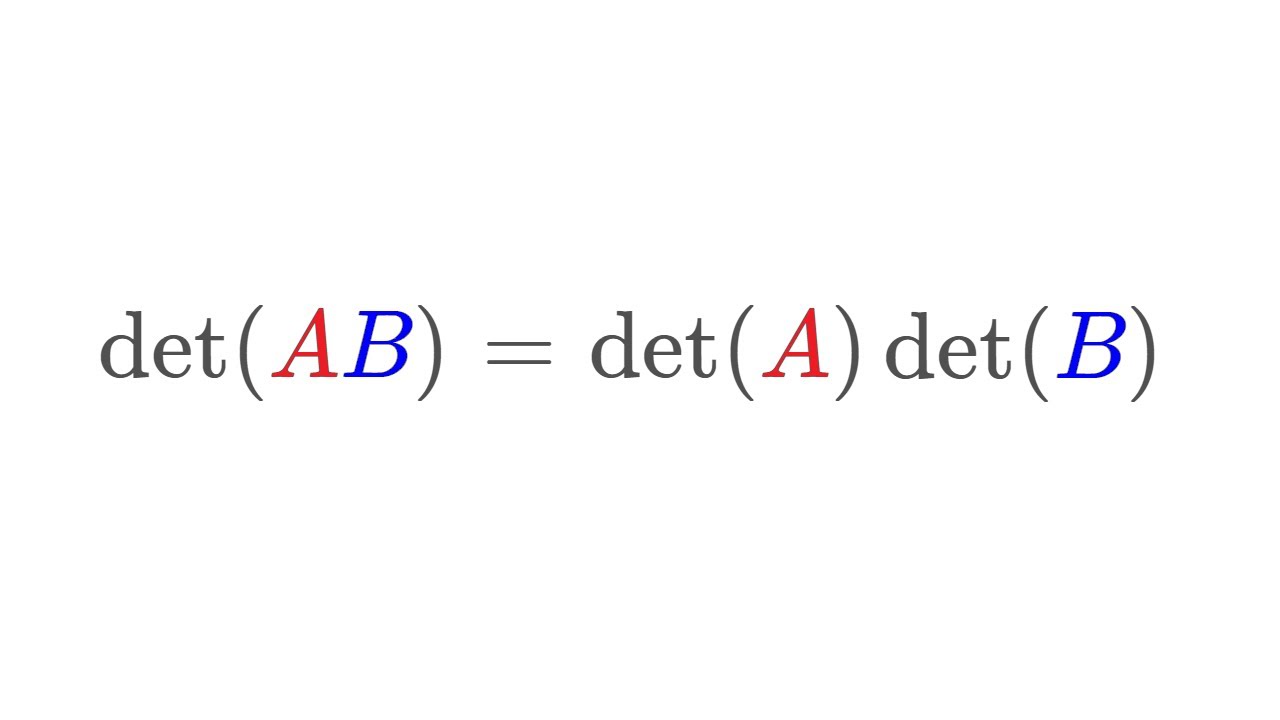
Показать описание

det(AB) = det(A) det(B)

In this video, I show why det(AB) = det(A) det(B). This video really illustrates why linear algebra is so neat. No messy calculations are required, just some useful facts about row reduction!

Рекомендации по теме

Комментарии

My linear algebra professor used elementary matrices to prove this fact too. It's often overlooked when you get an introduction to vectors and matrices how important bases are as assumptions to key proofs. The gift of linear algebra is freedom of perspective!!!! Love your Oprah frame picture for the dual basis video.

theproofessayist

não sei nem como parei aqui, mas é uma boa aula.. Parabens :)

luizeyuina

In Case 3 you meant to say using Case 2 instead of Case 1!?

compphysgeek

respect, I have a study guide that was just assigned today that Im doing a week before test

unbendedurchin

thank you very much PROFESSOR!!! GOD bless you. We expect you to continue to linear algebra proofs!!!

ugursoydan

I really like this view! I've always used 3blue1brown's geometric justification that the determinant can (almost?) be defined as the ratio of volume before transformation to volume after transformation. In that case, the determinant of the composition of two transformations leads to the product of the determinants of the underlying transformations. This is a totally different way of justifying the same fact, without really any geometry! I love math!

Keithfert

Very nice to have these linear algebra videos coming out right as I'm taking linear algebra!

SirGamestop

awesome proof, could not find a good one anywhere else

seanyboyblu

Your shirt is "I love Simon's factoring"? or just San Francisco

DiegoMathemagician

Hello thank you for this vidéo: 4:55 you say that in an other video you show that an invertible matrix can be written as product of elementary matrices. I don't find this video can you give me the link please.

rachidnajib

Nice, you look very determined to prove this theorem.

LuisBorja

omg loved it, so intuitive.
Isn't case 3, a proof by induction of case 2?

vpambspt

Your channel is always a joy to watch!

WizardOfArc

Thank u for this video can you proof that the charachteristic polynomial of AB is charachteristic polynomial of BA

mathsdusuperieur

I was just looking for this yesterday god bless ya

bamdadshamaei

So the determinant preserves “vector” multiplication. Like linear operators preserve addition and scalar multiplication. Is there some sort of analog to this preservation? Can this concept of multiplicative preservation be generalized to other operations? If so, would that be a useful branch of mathematics that could yield results that are applicable to other branches (I.e. linear algebra and differential equations)? Thanks for your awesome videos!

tylershepard

wow!! awesome intuitive explanation :)

mystic

Hello, I think when we want to find the inverse of a matrix we are not allowed tu use permutation of rows we can only add a multiple of a row to an other row or multiply a row by scalar why use interchange of rows 7:15

rachidnajib

I know this isnt really related, but like I need help with the hodge dual operator

donovanleyba

Wow, it was a cool proof. No messy calculations indeed. Neat :)

shayanmoosavi

det AB = det A det B

det AB = det A det B

Why does determinant (AB) = (det A) (det B)? - This Is Linear Algebra

A-Level Further Maths: C5-04 Determinants: Proving det(AB)=det(A)xdet(B) for 2x2 Matrices

det A + det B e det(A + B)

det A^T = det A

Linear Algebra Determinant Proof det(A^(-1)) = (detA)^(-1)

How should the determinant of AB relate to the product of det A and det B? - This Is Linear Algebra

Verificar que el det(AB)=(det A)(det B) para el siguiente par de matrices

A-Level Further Maths: C5-05 Determinants: Proving det(kA)=k^2det(A) for 2x2 Matrices

Let A and B be (3 `xx` 3) matrices with det A = 4 and det B = 3. What is det (2AB) equal to ?

A,B,C are 3 \times 3 matrices with det(A)=-3 , det(D)=-2, det(C)=6.What is det(A^2BC ... | Plainmath

Det A-1

Meine Mama ist... (DAS FINALE)

[Proof] det(B^-1AB) = det(A)

how to prove that det(adj(A))=(det(A))^n-1?

Det finns alltid en sån här person på varje arbetsplats. 😂 Trevlig helg finns på SVT Play....

Proof: If det(A) != 0 and AB = AC, then B = C

Det äne am Bärgli | Kinderlieder by ChinderMusigWält

11th Std Maths Ex.7.2(20) Verify det(AB) = det(A)det(B) for A= [ 4 3 2] and B= [ 1 3 3]

If A is semy square matrix of order 3 and det A = 5, then what is det`[(2A)^(-1)]` equal to ?

Cross products | Chapter 10, Essence of linear algebra

Det trodde jag aldrig

[Proof] If n is odd, then det(A) = 0 for skew-symmetric matrix

Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra