Proof: If det(A) != 0 and AB = AC, then B = C

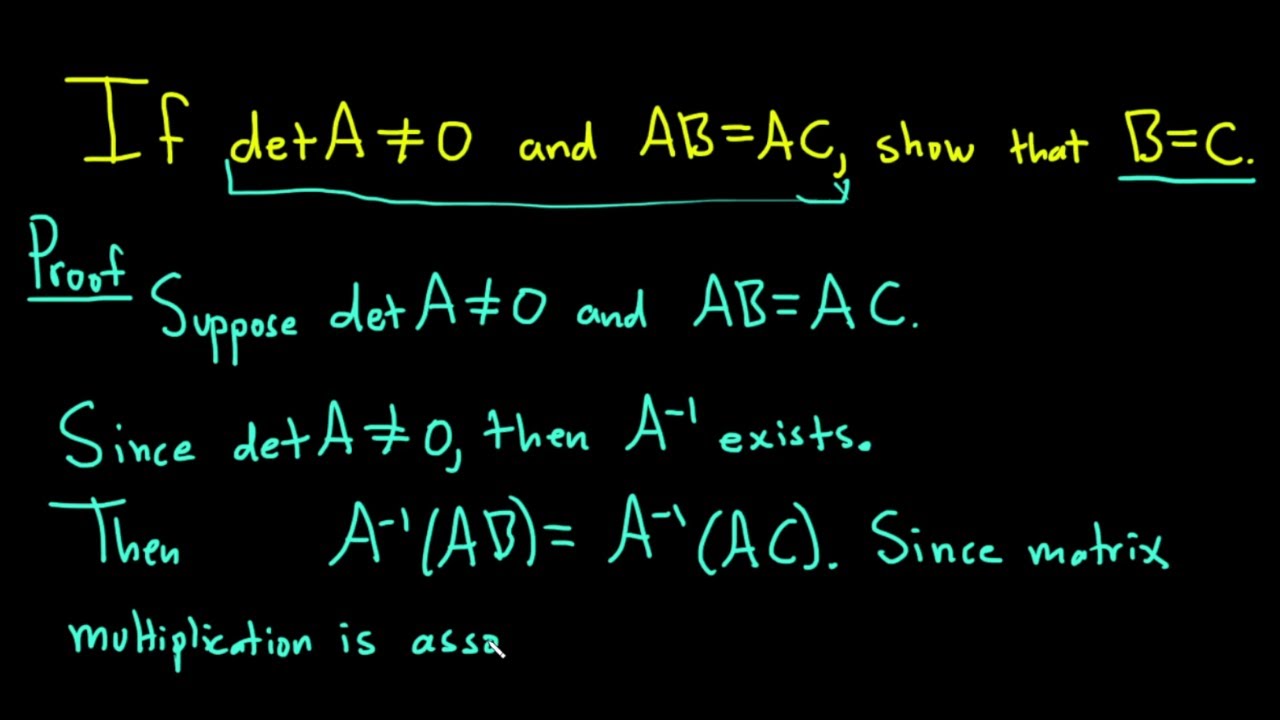
preview_player
Показать описание
We prove that if the determinant of a matrix A is nonzero and AB = AC, then we have that B = C. I hope this helps someone learning linear algebra.

(these are my affiliate links)

***********Math, Physics, and Computer Science Books***********
These are my affiliate links. As an Amazon Associate I earn from qualifying purchases.

If you enjoyed this video please consider liking, sharing, and subscribing.

There are several ways that you can help support my channel:)

************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course

Advanced Calculus Course

Calculus 1 Course

Calculus 2 Course

Calculus 3 Course

Calculus 1 Lectures with Assignments and a Final Exam

Calculus Integration Insanity

Differential Equations Course

Differential Equations Lectures Course (Includes Assignments + Final Exam)

College Algebra Course

How to Write Proofs with Sets Course

How to Write Proofs with Functions Course

Trigonometry 1 Course

Trigonometry 2 Course

Statistics with StatCrunch Course

Math Graduate Programs, Applying, Advice, Motivation

Daily Devotionals for Motivation with The Math Sorcerer

Thank you:)
  1. The Math Sorcerer
  2. linear algebra
  3. proof
Рекомендации по теме
Proof: If det(A) 0:03:59

Proof: If det(A) != 0 and AB = AC, then B = C

Proof: If the 0:04:13

Proof: If the inverse of A exists, the the determinant of A cannot be zero.

[Proof] If n 0:02:55

[Proof] If n is odd, then det(A) = 0 for skew-symmetric matrix

Show that there 0:01:55

Show that there is no B for det(A) = 0 and A * B equaling the Identity Matrix

Linear Algebra - 0:08:40

Linear Algebra - Proofs for Zero Determinant Theorems

If det(AB)=0, then 0:01:23

If det(AB)=0, then det(A)=0 or det(B) =0

Determinant Theorems and 0:05:31

Determinant Theorems and Proofs (part 3 of 4) - invertible

If det(A)=0, then 0:01:13

If det(A)=0, then det(AB)=0

Linear Algebra 14TBD: 0:03:58

Linear Algebra 14TBD: The Determinant is Zero ⇔ Matrix Is Singular

The determinant | 0:10:03

The determinant | Chapter 6, Essence of linear algebra

If matrix A 0:04:24

If matrix A has two identical rows then det(A)=0

Prove determinant is 0:00:57

Prove determinant is 0! #maths #algebra #matrix #determinants #proof #shorts

Determinant of Transpose: 0:04:32

Determinant of Transpose: Prove that det A^T = det A

Linear Algebra Determinant 0:01:22

Linear Algebra Determinant Proof det(A^(-1)) = (detA)^(-1)

Determinant of a 0:05:38

Determinant of a matrix is equal to product of eigenvalues. Proof and simple example.

What is a 0:02:51

What is a determinant?

Invertible iff Det 0:06:57

Invertible iff Det not 0

Prove using properties 0:04:55

Prove using properties of determinant problem 1

how to prove 0:04:44

how to prove that det(adj(A))=(det(A))^n-1?

Direct Proof of 0:13:22

Direct Proof of det(A)=det(A^T)

Proof of the 0:23:45

Proof of the Fact that det(AB)=(det A)(det B); Properties of Determinants

✅▶ DETERMINANT of 0:04:56

✅▶ DETERMINANT of a MATRIX by applying PROPERTIES

det A^T = 0:13:27

det A^T = det A

n x n 0:18:40

n x n determinant | Matrix transformations | Linear Algebra | Khan Academy

Комментарии
Автор

One might note that by imposing that det(A) =/= 0, we are forming a group, and the statement AB = AC => B = C is a general property of groups. Thus, this proof and concept are highly generalizable (its not actually about matrices _per se_ in its essence).

EpicMathTime