filmov
tv
Can you Solve it? High School Math Competition Problem

Показать описание
A high school math competition problem dealing with the Fibonnaci sequence.
9 Riddles Only People with High IQ Can Solve
You NEED a High IQ to Solve the Rubik's Cube
Can you solve the bridge riddle? - Alex Gendler
Can you Solve it? High School Math Competition Problem
Norway Math Olympiad Question | You should be able to solve this!
Can you solve the jail break riddle? - Dan Finkel
The Spaceships Paradox - Can You Solve It?
Can you solve the famously difficult green-eyed logic puzzle? - Alex Gendler
The Impossible Heist : Can you solve it ?
If you are genius solve this | Cool Maths Game
Can Tiny Gadgets Solve BIG Problems?
Even the Smartest Professor Can't Solve All 17 Riddles
7 Mystery Riddles Only the Smartest 5% Can Solve
Can you solve the egg drop riddle? - Yossi Elran
Can You Solve This Murder?
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Can you solve the birthday cake riddle? - Marie Brodsky
If you are a genius solve this! Math Game Challenge!!!
Can You Solve This?
Can you solve this 150 years old puzzle? #shorts
Can you solve the frog riddle? - Derek Abbott
Can you solve the passcode riddle? - Ganesh Pai
Can you solve the locker riddle? - Lisa Winer
Solve These Riddles, and You're a Math Genius
Комментарии
 0:11:51
0:11:51
 0:10:08
0:10:08
 0:03:50
0:03:50
 0:01:33
0:01:33
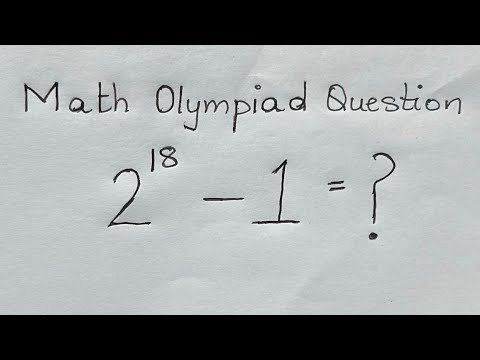 0:03:21
0:03:21
 0:03:25
0:03:25
 0:11:24
0:11:24
 0:04:42
0:04:42
 0:00:58
0:00:58
 0:01:54
0:01:54
 0:11:05
0:11:05
 0:12:23
0:12:23
 0:09:12
0:09:12
 0:04:47
0:04:47
 0:04:28
0:04:28
 0:22:09
0:22:09
 0:04:48
0:04:48
 0:00:28
0:00:28
 0:01:47
0:01:47
 0:00:57
0:00:57
 0:04:31
0:04:31
 0:04:08
0:04:08
 0:03:50
0:03:50
 0:16:03
0:16:03