QIP2021 | Random quantum circuits anti-concentrate in log depth (Alexander Dalzell)

Authors: Alexander Dalzell, Nicholas Hunter-Jones and Fernando Brandão
Affiliations: California Institute of Technology | Perimeter Institute for Theoretical Physics | AWS Center for Quantum Computing

Abstract:
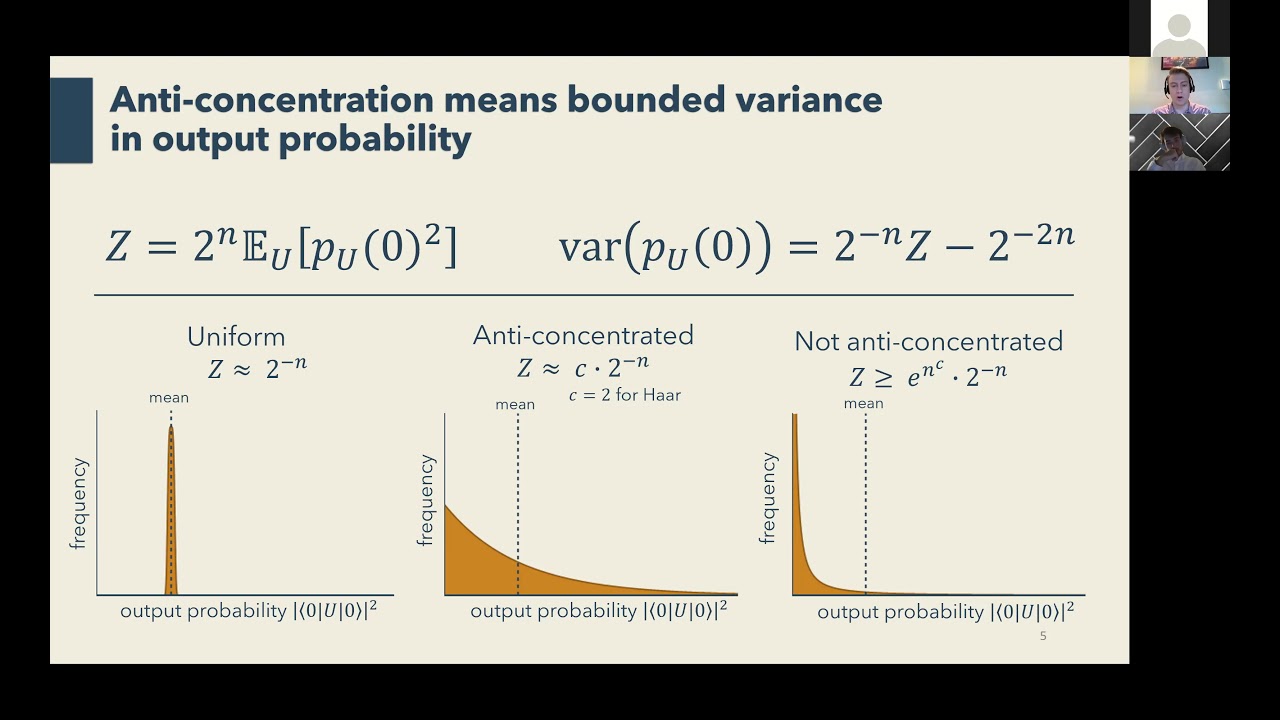
We consider quantum circuits consisting of randomly chosen two-local gates and study the number of gates needed for the distribution over measurement outcomes for typical circuit instances to be anti-concentrated, roughly meaning that the probability mass is not too concentrated on a small number of measurement outcomes. Understanding the conditions for anti-concentration is important for determining which quantum circuits are difficult to simulate classically, as anti-concentration has been in some cases an ingredient of mathematical arguments that simulation is hard and in other cases a necessary condition for easy simulation. Our definition of anti-concentration is that the expected collision probability, that is, the probability that two independently drawn outcomes will agree, is only a constant factor larger than if the distribution were uniform. We show that when the 2-local gates are each drawn from the Haar measure (or any two-design), at least O(n log(n)) gates (and thus O(log(n)) circuit depth) are needed for this condition to be met on an n qudit circuit. In both the case where the gates are nearest-neighbor on a 1D ring and the case where gates are long-range, we show O(n log(n)) gates are also sufficient, and we precisely compute the optimal constant prefactor for the n log(n). The technique we employ relies upon a mapping from the expected collision probability to the partition function of an Ising-like classical statistical mechanical model, which we manage to bound using stochastic and combinatorial techniques.

Get entangled with us!