filmov
tv
Multivariable Calculus 14 | Vector Fields and Potential Functions

Показать описание
Please consider to support me if this video was helpful such that I can continue to produce them :)
🙏 Thanks to all supporters! They are mentioned in the credits of the video :)
The video is about how potentials work in higher dimensions.
#MultivariableCalculus
#Analysis
#Integral
#Calculus
#Derivatives
#Mathematicspdt
#Lagrange
(This explanation fits to lectures for students in their first year of study: Mathematics for physicists, Mathematics for the natural science, Mathematics for engineers and so on)
Multivariable Calculus 14 | Vector Fields and Potential Functions
Multivariable Calculus 14 | Vector Fields and Potential Functions [dark version]
Multivariable Calculus 14 1 Vector Functions
Calculus 3 Lecture 13.1: Intro to Multivariable Functions (Domain, Sketching, Level Curves)
Vectors, Vector Fields, and Gradients | Multivariable Calculus
Multivariable chain rule | Lecture 14 | Vector Calculus for Engineers
Partial Derivatives - Multivariable Calculus
14.1 Domain and range for multi-variable functions
Super THIN Vector Calculus Book
Multivariable Calculus 14 2 Derivatives and Integrals of Vector Functions
Angle between vectors leads to defining the Dot Product | Multivariable Calculus
Calculus 3 Lecture 13.3: Partial Derivatives (Derivatives of Multivariable Functions)
14: Directional Derivatives and Gradient - Valuable Vector Calculus
Limits of Multivariable Functions - Calculus 3
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
Position vector valued functions | Multivariable Calculus | Khan Academy
Geometric Meaning of the Gradient Vector
Constructing a unit normal vector to a surface | Multivariable Calculus | Khan Academy
Vector Magnitude and the Standard Basis Vectors, Multivariable Calculus Unit 1 Lecture 05
Super Famous Book on Vector Calculus
What is a gradient? Explained in under one minute
Multivariable Calculus | The projection of a vector.
Vector valued function derivative example | Multivariable Calculus | Khan Academy
How REAL Men Integrate Functions
Комментарии
 0:06:58
0:06:58
 0:06:58
0:06:58
 0:10:37
0:10:37
 1:49:07
1:49:07
 0:20:26
0:20:26
 0:09:19
0:09:19
 1:00:33
1:00:33
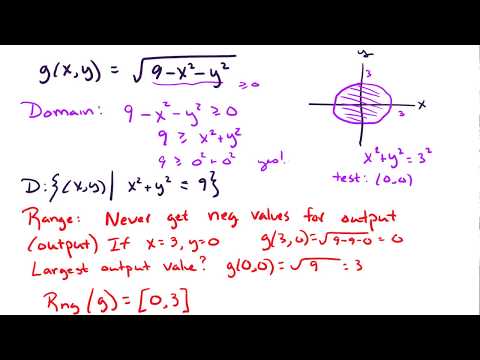 0:10:45
0:10:45
 0:01:00
0:01:00
 0:10:17
0:10:17
 0:06:11
0:06:11
 2:28:53
2:28:53
 0:07:59
0:07:59
 0:19:04
0:19:04
 0:11:24
0:11:24
 0:07:45
0:07:45
 0:14:51
0:14:51
 0:06:23
0:06:23
 0:18:49
0:18:49
 0:00:52
0:00:52
 0:00:49
0:00:49
 0:09:30
0:09:30
 0:12:45
0:12:45
 0:00:35
0:00:35