filmov
tv
Abstract Algebra, Lec 6B: Subgroup Tests, Cyclic Subgroups, Center of a Group, Cyclic Groups
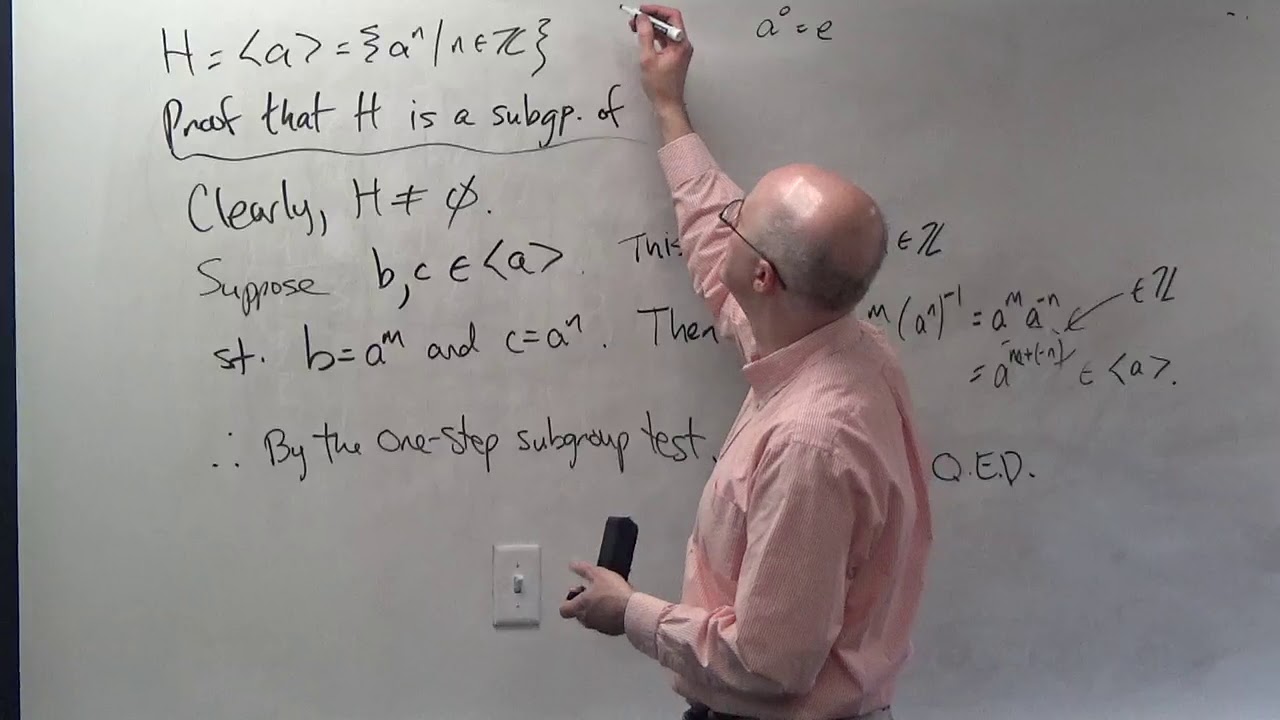
Показать описание
(0:00) Cayley table for Z6 rearranged to emphasize that {0,2,4} is a subgroup of Z6 under addition mod 6.
(3:53) Cyclic subgroup of G generated by an element "a".
(6:15) Analogy with vector spaces: one-dimensional subspace (spanned by one vector) in the vector space.
(7:45) Use the one-step subgroup test to prove that the cyclic subgroup generated by "a" is truly a subgroup (need to test that the given set is nonempty first).
(14:36) Two-step subgroup test.
(15:26) Finite subgroup test.
(15:55) Infinite groups can have finite subgroups (even beyond the trivial subgroup).
(17:18) {1,i,-1,-i} is a cyclic subgroup of order 4 of C - {0}: it has i = sqrt(-1) as a generator.
(18:50) Center of G is a subgroup of G (the center is the set of all elements of G that commute with everything in G) and idea of how to use the two-step subgroup test to prove it.
(27:32) Definition of a cyclic group and consider examples: Z is cyclic, Z6 is cyclic, Zn is cyclic (1 and n-1 are always generators, though there could be other generators, especially when n is prime), U(10) = {1,3,7,9} is cyclic (under multiplication mod 10), but U(8) is not cyclic (under multiplication mod 8).
(31:26) Note that cyclic groups must be Abelian, so non-Abelian groups are not cyclic.
AMAZON ASSOCIATE
As an Amazon Associate I earn from qualifying purchases.
Комментарии
 0:31:52
0:31:52
 0:11:24
0:11:24
 0:09:24
0:09:24
 0:10:46
0:10:46
 0:09:01
0:09:01
 0:09:19
0:09:19
 0:14:33
0:14:33
 0:05:30
0:05:30
 0:06:39
0:06:39
 0:27:50
0:27:50
 0:14:10
0:14:10
 0:49:13
0:49:13
 0:18:24
0:18:24
 0:12:15
0:12:15
 0:06:10
0:06:10
 0:10:18
0:10:18
 0:08:53
0:08:53
 0:30:45
0:30:45
 0:13:27
0:13:27
 0:33:37
0:33:37
 0:13:03
0:13:03
 1:02:54
1:02:54
 0:34:35
0:34:35
 0:27:48
0:27:48