Inverse Functions | MathHelp.com

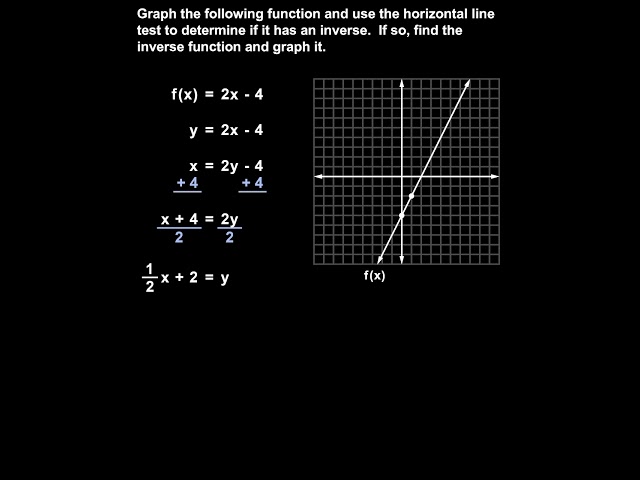
Here we’re asked to graph the following function and use the horizontal line test to determine if it has an inverse. And if so, find the inverse function and graph it. So let’s start by graphing the given function, f(x) = 2x – 4, and remember that f(x) is the same as y, so we can rewrite the function as y = 2x – 4. Now, we simply graph the line y = 2x – 4, which has a y-intercept of -4, and a slope of 2, or 2/1, so we go up 2 and over 1, plot a second point and graph our line, which we’ll call f(x). Next, we’re asked to use the horizontal line test to determine if the function has an inverse. Since there’s no way to draw a horizontal line that intersects more than one point on the function, the function does have an inverse. So we need to find the inverse and graph it. To find the inverse, we switch the x and the y in original function, y = 2x – 4, to get x = 2y – 4. Next, we solve for y, so we add 4 to both sides to get x + 4 = 2y, and divide both sides by 2 to get 1/2x + 2 = y. Next, let’s flip our equation so that y is on the left side, and we have y = 1/2x + 2. Finally, we replace y with the notation that we use for the inverse function of f, as shown here. And remember that we’re asked to graph the inverse as well, so we graph y = ½ x + 2. Our y-intercept is positive 2, and our slope is ½, so we go up one and over 2, plot a second point, graph the line, and label it as the inverse function of f. Notice that the graph of the inverse function is a reflection of the original function in the line y = x.