L23.4 Symmetric and Antisymmetric states of N particles

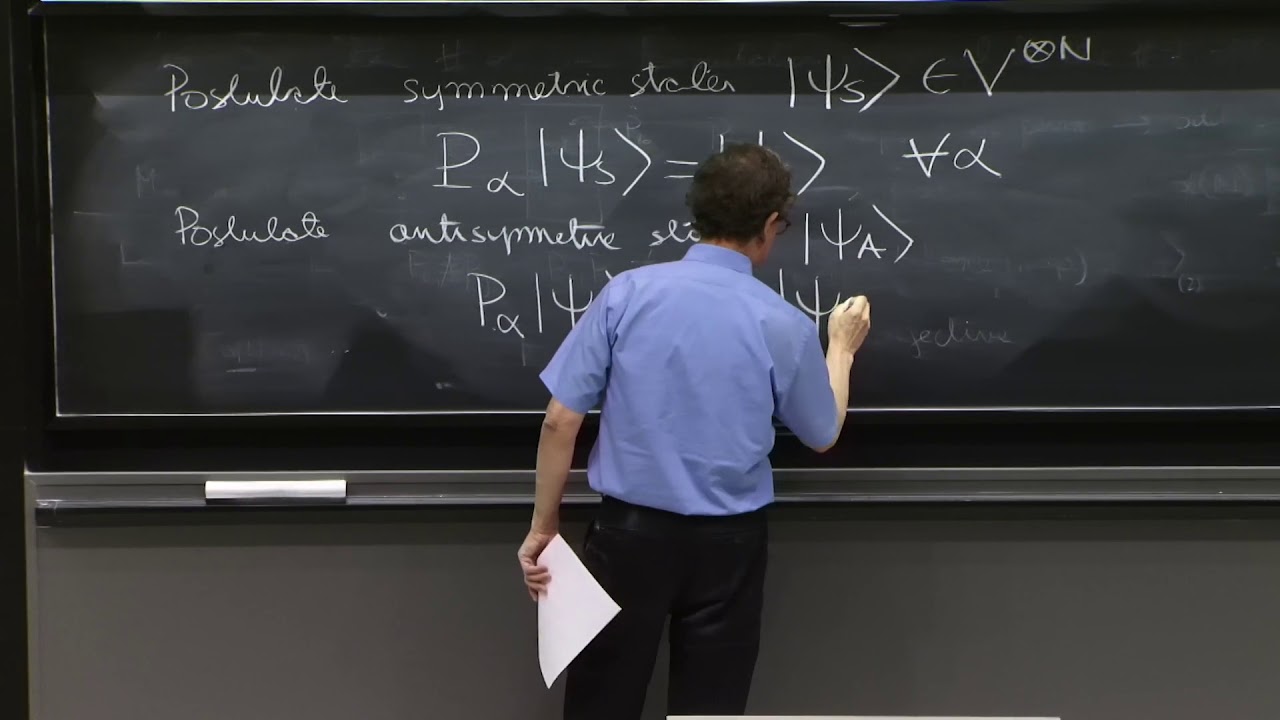
preview_player
Показать описание
MIT 8.06 Quantum Physics III, Spring 2018
Instructor: Barton Zwiebach

L23.4 Symmetric and Antisymmetric states of N particles

License: Creative Commons BY-NC-SA
  1. MIT OpenCourseWare
  2. identical particles
  3. symmetric states
  4. antisymmetric states
  5. N particles
Рекомендации по теме
L23.4 Symmetric and 0:11:35

L23.4 Symmetric and Antisymmetric states of N particles

Symmetric and Anti-symmetric 0:13:12

Symmetric and Anti-symmetric Wave functions

Symmetric and antisymmetric 0:14:45

Symmetric and antisymmetric states of many quantum particles

Types of Relations 0:06:39

Types of Relations (Part 1)

Symmetric and Antisymmetric 0:01:59

Symmetric and Antisymmetric Matrices

Antisymmetric relation 0:02:25

Antisymmetric relation

Anti symmetry 0:01:28

Anti symmetry

Symmetric & Anti-Symmetric 0:00:16

Symmetric & Anti-Symmetric #shorts #plz subscribe #S.M

Symmetric and antisymmetric 0:19:29

Symmetric and antisymmetric wavefunction: Bose Einstein and Fermi-Dirac statistics

21 3 Wavefunctions 0:14:29

21 3 Wavefunctions of Electrons Are Antisymmetric

Symmetry of wavefunction 0:03:13

Symmetry of wavefunction

DMA 2.8.2 Symmetric 0:27:41

DMA 2.8.2 Symmetric and Anti-symmetric

Diagram 502a WOW! 0:00:57

Diagram 502a WOW! Anti-Symmetric Fermionic Wave Particles

10. CONJUCATE SYMMETRIC 0:07:10

10. CONJUCATE SYMMETRIC AND ANTISYMMETRIC SIGNALS

L24.1 Symmetrizer and 0:16:50

L24.1 Symmetrizer and antisymmetrizer for N particles

SYMMETRIC AND ANTISYMMETRIC 0:12:45

SYMMETRIC AND ANTISYMMETRIC

Purdue PHYS 342 0:21:36

Purdue PHYS 342 L7.4: Pauli's Exclusion Principle: Wavefunction Symmetry

The Antisymmetry Property 0:05:21

The Antisymmetry Property of Determinants - Linear Algebra Ch1.4 Part 3

Quantum Chemistry 9.5 0:04:59

Quantum Chemistry 9.5 - Antisymmetry Principle

Indistinguishable Particles and 0:11:37

Indistinguishable Particles and Symmetry (PHAS3226 Video 23)

Quantum mechanics|Spin orbital 0:12:54

Quantum mechanics|Spin orbital & their linear combination|the symmetric and antisymmetric spin f...

L23.4 Where is 0:05:00

L23.4 Where is an Arrival of the Merged Process Coming From?

Exchange Antisymmetry 0:15:26

Exchange Antisymmetry

L24.3 The symmetrization 0:11:39

L24.3 The symmetrization postulate

Комментарии
Автор

Why does Prof Zwiebach *postulate* that identical particles have totally symmetric or anti-symmetric wave functions? In other courses, including the one by Allan Adams, that fact is "derived" from the idea that there is no experiment you can do to distinguish the particles. Not being able to distinguish by means of any experiment is taken to mean |psi(a, b)| = |psi(b, a)|, ie the probabilities are equal.

TBH, the motivation for this probability argument (the one from Allan Adams) always bothered me. The motivation I'm assuming is that if P(a, b) != P(b, a), then certain orderings of measurements would be less probable than others, so (7 meters, 8 meters) not as likely as the reverse. But I thought that when I make a measurement of identical particles, I get an *unordered* list of numbers, because I can't tell which particle now has each value. They're identical .

Any help would be appreciated, and I'm sorry if what I'm asking isn't clear.

physicsguy
Автор

1:36 "The majority are -a- unitary."
5:41 "You cannot expect -the- *a* basis."

cikif