filmov
tv
Symmetric and antisymmetric states of many quantum particles

Показать описание
Symmetric and antisymmetric states describe quantum systems of identical particles.
📚 In this video we define totally symmetric and totally antisymmetric states. Totally symmetric states stay the same when we exchange any two particles, while totally antisymmetric states get an extra minus sign when we exchange any two particles. Their properties make them the only quantum states that can describe systems of identical particles. We will also learn how to build these states, using the so-called symmetrizer and antisymmetrizer operators. Finally, we will define totally symmetric operators, that do not change under the exchange of particles. All these ideas will allow us to study the quantum mechanics of systems of identical particles.
⏮️ BACKGROUND
⏭️ WHAT NEXT?
~
Director and writer: BM
Producer and designer: MC
📚 In this video we define totally symmetric and totally antisymmetric states. Totally symmetric states stay the same when we exchange any two particles, while totally antisymmetric states get an extra minus sign when we exchange any two particles. Their properties make them the only quantum states that can describe systems of identical particles. We will also learn how to build these states, using the so-called symmetrizer and antisymmetrizer operators. Finally, we will define totally symmetric operators, that do not change under the exchange of particles. All these ideas will allow us to study the quantum mechanics of systems of identical particles.
⏮️ BACKGROUND
⏭️ WHAT NEXT?
~
Director and writer: BM
Producer and designer: MC
L23.4 Symmetric and Antisymmetric states of N particles
Symmetric and antisymmetric states of many quantum particles
Symmetric and Anti-symmetric Wave functions
Question on Symmetric and Anti-symmetric states.
Quantum Chemistry 9.5 - Antisymmetry Principle
Symmetric and antisymmetric wave function
Symmetric and antisymmetric wave function
Types of Relations (Part 1)
Symmetric and Antisymmetric Matrices
8.16-Singlet Triplet States
Symmetric and Anti symmetric wave functions- Semester 1 M.Sc Chemistry, MGU Kottayam
Symmetric and antisymmetric wavefunction: Bose Einstein and Fermi-Dirac statistics
Quantum Mechanics: Symmetric and antisymmetric combination of spin half. Triplet and singlet states.
B.Sc HP4 - Identical particles : Symmetric and Antisymmetric wavefuction
Symmetry of wavefunction
Bosons and fermions: the symmetrization postulate
Symmetric and Antisymmetric wavefunction
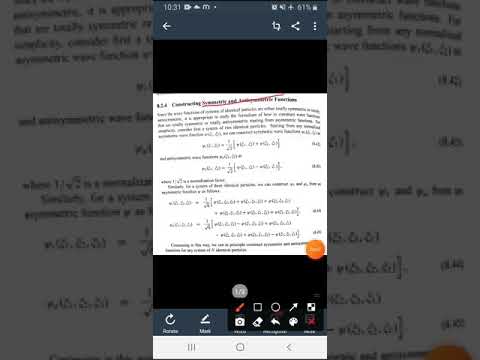
Constructing Symmetric & Antisymmetric Functions by Nidhi Sharma from Quantum Mechanics
Symmetric and antisymmetric wave function
pauli's exclusion principle || symmetric and asymmetric wave function
Identical Particles /symmetric and anti symmetric wave function/Quantum Physics/
Tensors as a Sum of Symmetric and Antisymmetric Tensors
Symmetric and antisymmetric wavefunctions: Statistical mechanics 22 Reference R K Pathria
Symmetric & Anti-Symmetric wave function S.M
Комментарии
 0:11:35
0:11:35
 0:14:45
0:14:45
 0:13:12
0:13:12
 0:03:03
0:03:03
 0:04:59
0:04:59
 0:10:35
0:10:35
 0:07:31
0:07:31
 0:06:39
0:06:39
 0:01:59
0:01:59
 0:17:12
0:17:12
 0:08:29
0:08:29
 0:19:29
0:19:29
 0:12:54
0:12:54
 0:30:02
0:30:02
 0:03:13
0:03:13
 0:17:47
0:17:47
 0:28:14
0:28:14
 0:03:43
0:03:43
 0:15:41
0:15:41
 0:05:03
0:05:03
 0:37:02
0:37:02
 0:09:47
0:09:47
 0:41:27
0:41:27
 0:01:12
0:01:12