filmov
tv
The Mandelbrot Set - Numberphile

Показать описание
Famously beautiful, the Mandelbrot Set is all about complex numbers. Featuring Dr Holly Krieger from MIT.
More links & stuff in full description below ↓↓↓
Since this was filmed, Holly has become a mathematics Lecturer at the University of Cambridge and the Corfield Fellow at Murray Edwards College.
NUMBERPHILE
Videos by Brady Haran
More links & stuff in full description below ↓↓↓
Since this was filmed, Holly has become a mathematics Lecturer at the University of Cambridge and the Corfield Fellow at Murray Edwards College.
NUMBERPHILE
Videos by Brady Haran
The Mandelbrot Set - Numberphile
What's so special about the Mandelbrot Set? - Numberphile
Fibonacci Numbers hidden in the Mandelbrot Set - Numberphile
Pi and the Mandelbrot Set - Numberphile
Decoding The Mandelbrot Set: Math’s Famed Fractal
Beyond the Mandelbrot set, an intro to holomorphic dynamics
Proving God exists using Math
63 and -7/4 are special - Numberphile
The Mandelbrot Set
How to Calculate a Mandelbrot Set
Convergence of the Mandelbrot set
The Mandelbrot Set: How it Works, and Why it's Amazing!
This Shape Reveals How God Thinks
Have you ever found 'fibonacci series' on Mandelbrot Fractals in the form of patterns? #fr...
The Feigenbaum Constant (4.669) - Numberphile
Filled Julia Set
'Trypophobic' - music from Numberphile's Mandelbrot Set
The Mandelbrot Set: Atheists’ WORST Nightmare
The Mandelbrot Set
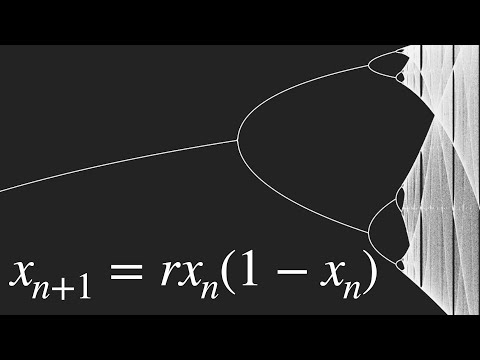
This equation will change how you see the world (the logistic map)
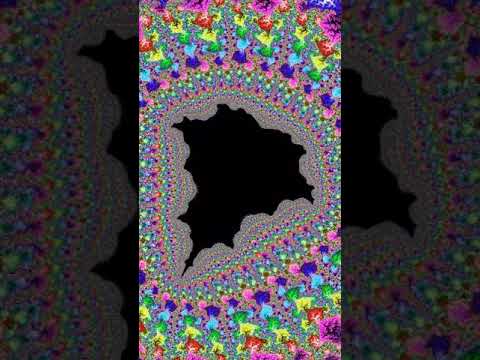
mandelbrot set #shorts test
The Opposite of Infinity - Numberphile
Pi and Mandelbrot (extra footage)
Level of the Day: Mandelbrot Set
Комментарии
 0:09:11
0:09:11
 0:16:53
0:16:53
 0:09:59
0:09:59
 0:07:56
0:07:56
 0:08:08
0:08:08
 0:27:36
0:27:36
 0:05:23
0:05:23
 0:12:13
0:12:13
 0:15:30
0:15:30
 0:00:59
0:00:59
 0:00:06
0:00:06
 0:04:05
0:04:05
 0:00:58
0:00:58
 0:01:01
0:01:01
 0:18:55
0:18:55
 0:06:48
0:06:48
 0:02:32
0:02:32
 0:38:25
0:38:25
 0:00:25
0:00:25
 0:18:39
0:18:39
 0:00:54
0:00:54
 0:15:05
0:15:05
 0:06:56
0:06:56
 0:00:08
0:00:08