Fundamental Rank Theorem

preview_player
Показать описание
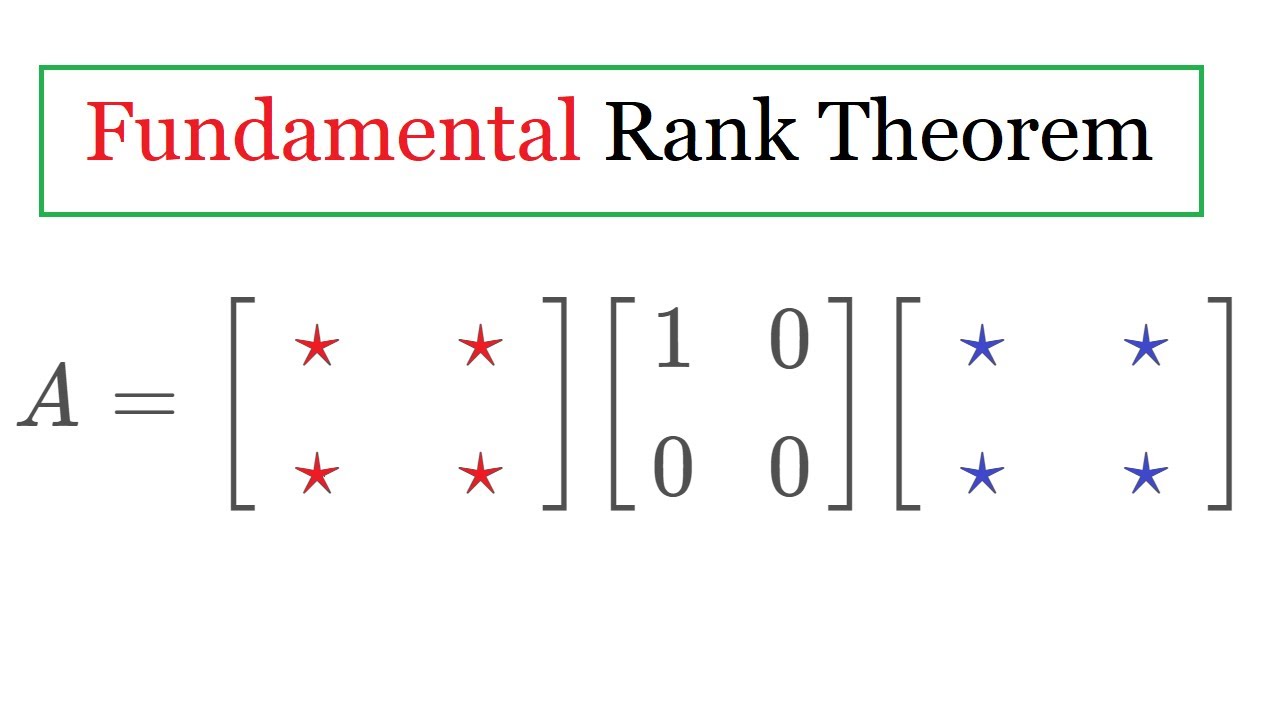
In this video, I state and prove the Fundamental Rank Theorem, one of the cornerstones of the theory of linear equations. This theorem says that any matrix can be row and column reduced to a matrix with only 1's and 0's on the diagonal, where the number of 1's is equal to the rank of the matrix. In future videos (on this playlist), I'll discuss some applications of this theorem.

  1. Dr Peyam
  2. math
  3. mathematics
  4. peyam
  5. dr peyam
  6. bprp
Рекомендации по теме
Fundamental Rank Theorem 0:18:06

Fundamental Rank Theorem

The rank nullity 0:03:16

The rank nullity relation and examples

Inverse matrices, column 0:12:09

Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra

The Dimension Theorem 0:04:02

The Dimension Theorem | Dim(Null(A)) + Dim(Col(A)) = n | Also, Rank!

Introduction to Rank 0:10:34

Introduction to Rank Theorem

SFU MATH 232 0:34:02

SFU MATH 232 7.5 The Rank Theorem

Rank-Nullity Theorem 0:09:09

Rank-Nullity Theorem

The rank theorem 0:08:02

The rank theorem - proof

The Rank Nullity 0:04:36

The Rank Nullity Theorem

Rank Nullity Theorem 0:12:50

Rank Nullity Theorem

Rank Theorem (Rank-Nullity 0:36:59

Rank Theorem (Rank-Nullity Thm), 4 Fundamental Subspaces, Invertible Matrix Theorem, Change of Basis

The Four Fundamental 0:21:45

The Four Fundamental Subspaces and the Fundamental Theorem | Linear Algebra

The Rank Theorem 0:12:48

The Rank Theorem (Example 1)

The Fundamental Theorem 0:13:53

The Fundamental Theorem of Linear Algebra

State and apply 0:04:22

State and apply the fundamental theorem of linear maps

Using the Rank 0:44:30

Using the Rank - Nullity Theorem

Rank Theorem 0:09:54

Rank Theorem

The Rank Theorem 0:04:59

The Rank Theorem

Rank-Nullity Intuition | 0:10:34

Rank-Nullity Intuition | Rank-Nullity Theorem for Vector Space

Lecture 18 : 0:21:56

Lecture 18 : Fundamental Theorem of Vector Space Homomorphism and Rank-Nullity Theorem

Rank Nullity Theorem 0:11:39

Rank Nullity Theorem Examples & Verification

Rank of Matrix 0:05:20

Rank of Matrix Explained in Hindi | Engineering Mathematics

state and prove 0:00:09

state and prove rank nullity theorem important theorem Bsc ba 5sem differential geometry

3) Fundamental Theorem 0:29:00

3) Fundamental Theorem of Vector Space Homomorphism (Lecture 3) #Rank and Nullity #Linear Algebra

Комментарии
Автор

Big fan of yours, from india#mathsbeetle

Matchless_gift
Автор

We are both mathematicians and lefties.... I'm very impressed. Well done

sammykmfmaths
Автор

Great proof and examples!!! But, I wonder if you could give a more rigorous proof next time for us to review as the way you did in class such that we know what we are expected to write on our exams. Anyhow, your video gave a clear idea and direction on how to prove the theorem :) Love it.

haohanliu
Автор

Sir, can you talk about
" Why matrix is needed in Mathematics" in a separate video, please? I want to know about it.

IshaaqNewton
Автор

is it really important to transform the matrix A to a particular matrix D? in my class, it only need to use row reduction and change it into reduced row echelon

rizkyagungshahputra