Rank Nullity Theorem

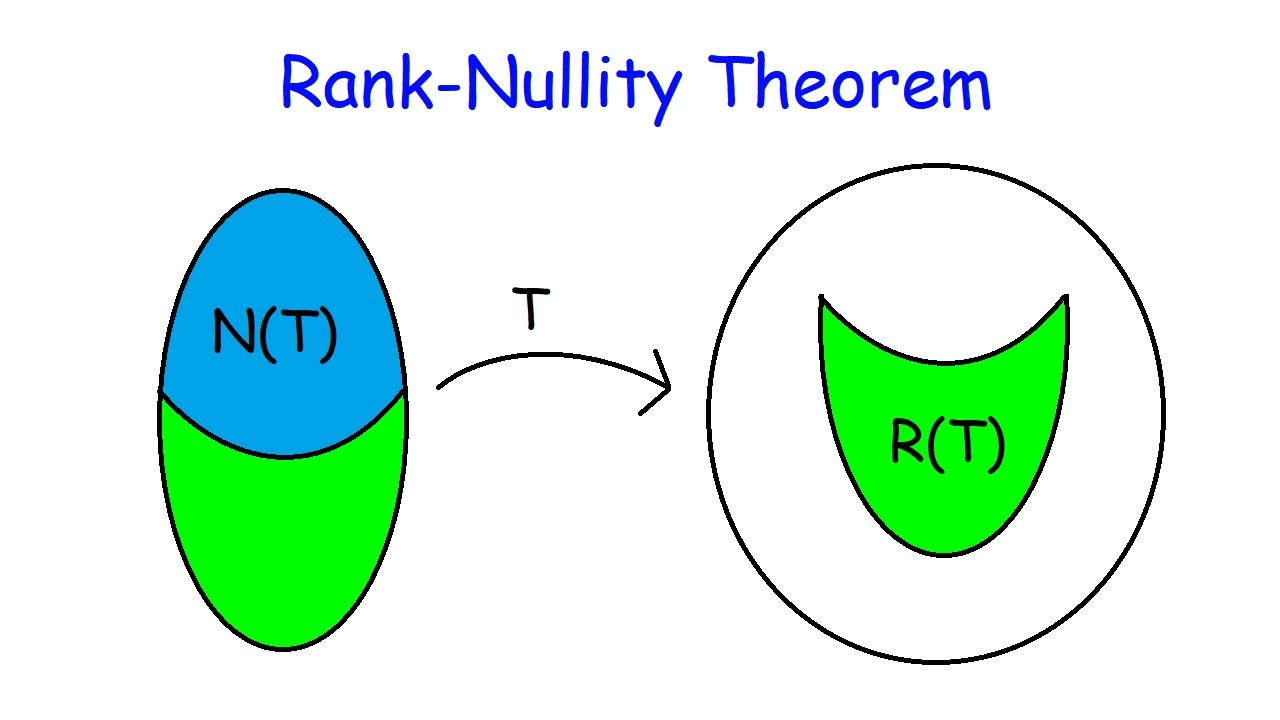
Proof of the Rank-Nullity Theorem, one of the cornerstones of linear algebra. Intuitively, it says that the rank and the nullity of a linear transformation are related: the more vectors T sends to 0, the smaller its range. The proof is especially elegant and uses important concepts in linear algebra, like basis extension, range, and linear independence. Enjoy!

[sergiocampero]

I'm starting to study Linear Algebra, and then you appear with this awesome video, and I can't be happier. Thank you very much. Also, I love your character and your humbleness.

[shayanmoosavi]

Wow, neat proof. The more I study linear algebra the more it makes sense. It's such a beautiful subject and I fell in love with it. It relates to most of the concepts in calculus and differential equations and I'm starting to realize why some of those concepts work. I started self studying linear algebra about a month ago and I think I learned most of the essential things to help me in my major which is engineering physics.

I realized that some of our physics courses such as mathematical physics (Sometimes called mathematical methods for physics) rely heavily on linear algebra and our curriculum (surprisingly) doesn't include a linear algebra course.

since our university started online courses (which absolutely sucks by the way and my classmates and I are going to abort this semester soon) because of the coronavirus outbreak, in about two months I learned more concepts (mostly linear algebra) than a whole semester.

[vukstojiljkovic]

Dam i love this proof, we did it in the class but the teacher didnt explain it that good. I love it how you used pictures to explain whats going on!

[leonardromano]

Wow, it is also one of my favourite theorems in LA. It just gets so intuitive and also so useful.

[mmorizes]

I don't know if it's nostalgia or a case of looking at the past with rose-tinted glasses, but the older courses in my undergraduate studies seem so much more beautiful and easy to understand in retrospect. Even analysis II seems like it won't make me want to wish I was in Dante's inferno.

[MrCigarro]

Brilliant proof. Thank you. This theorem is fundamental because every model that has a probabilistic component or error dimensión, which is the null space.

[jenniejisookim]

Hello Dr. Peyam, I realize this video is really old so I'm not sure if I'll receive a reply back, but I was wondering what the "b" is referring to at around 8:20
The video states that (a_m+1)(v_m+1) + .... + (a_n)(v_n) = (b_1)(v_1) + .... + (b_m)(v_m)

Thank you for all your videos! It's been tremendous help for me to study for lin alg.

[DP-sqlw]

It's just so beautiful. I have no word to describe it!

[Mrphsm]

Very nice proof! But do we really need W to be finite dimensional? I think it would suffice to assume that dim(V) < infinity. Furthermore could we make the proof work for a countably infinite dimensional V? Or even uncountable?

[brianvirgin]

Linear algebra was one of my favorite subjects.

[andreea-teodoragrecu]

Thank you very much! It was very helpful!!

[GRosa]

Dr P: Here's a proof of the rank-nullity theorem...
Me: whoosh! 😅

[abhijeetshukla]

Excellent way of explanation

Also quite energetic 😍🧡🔥

[theproofessayist]

I'm going to think of Rank Nullity Theorem in terms of Chinese Yin and Yang now Dr Peyam hahahaha! :)

[yhmah]

Bah du coup c’est quoi la différence entre nul(f) et ker(f) ? Ceci dit le théorème ressemble beaucoup au théorème du rang (peut-être aussi parce que C’EST le théorème du rang)