filmov
tv
Solving x^(2/3)=64

Показать описание
How do we solve x^(2/3)=64? In this algebra tutorial, we will see how to solve an equation with a rational exponent. We can either do it from the exponent way (but we may make careless mistakes) or change it to the radical form first then solve. This is the type of equations you will encounter in Algebra 2 and Precalculus!
-----------------------------
-----------------------------
#math #algebra #mathbasics
-----------------------------
-----------------------------
#math #algebra #mathbasics
Solving x^(2/3)=64
Nice Olympiad Exponential Equation X^x=2^64 | Solve In 1 Minute
Solve the Exponential Equation 2^x = 64
Factoring x^2-64, x^3-64, and x^6-64
How to factor a polynomial using the difference of two cubes
How to solve an equation with fraction powers in your exponent
Linear equation with one unknown: Solve 97=1/3(x)+2/3(64) step-by-step solution
Expanding Brackets
Mixed & Improper Fractions question
A Nice Math Olympiad Exponential Equation 3^x = X^9
Multiples of 8 😎 #Shorts #math #maths #mathematics
Exponential Equations - Algebra and Precalculus
Human Calculator Solves World’s Longest Math Problem #shorts
#exponent #indices #solve | If ( X-1)¾= 64, find X | Exponential Equation | Exponent and Power
Can You spot the Fake Rubik’s Cube? 🤔
Learn how to evaluate for a function
@ptsclasses Solve It: 3(x+6)+2 (x+3) = 64
Factoring Special Product “𝑥^3 + 64” | Step-by-Step Algebra Solution - Math Doodle
This trick can make your rubik's cube 2x faster😱🔥#ytshorts#shorts#drcuber
Algebra: FOIL Method #Shorts #algebra #math #maths #mathematics #education #learn
9 TIMES TABLE #shorts #math #maths #mathematics
3+6 divided by 2 = 6??
Simplify
Equations involving Indices
Комментарии
 0:03:18
0:03:18
 0:01:37
0:01:37
 0:00:34
0:00:34
 0:05:33
0:05:33
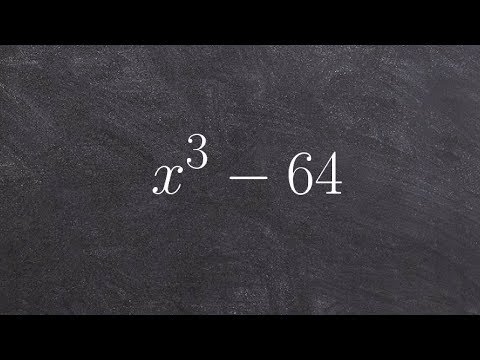 0:02:21
0:02:21
 0:03:47
0:03:47
 0:02:03
0:02:03
 0:00:51
0:00:51
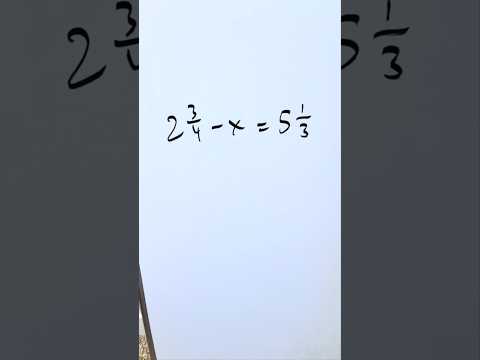 0:00:59
0:00:59
 0:02:34
0:02:34
 0:00:20
0:00:20
 0:05:58
0:05:58
 0:00:34
0:00:34
 0:01:25
0:01:25
 0:00:20
0:00:20
 0:02:15
0:02:15
 0:01:57
0:01:57
 0:01:00
0:01:00
 0:00:16
0:00:16
 0:00:18
0:00:18
 0:00:23
0:00:23
 0:00:10
0:00:10
 0:05:21
0:05:21
 0:06:10
0:06:10