filmov
tv
How to Read Logic

Показать описание
Symbolic logic looks intimidating, combining familiar symbols like equality and inclusion with lesser-known backwards E’s and upside down A’s. But with a bit of guidance, anyone can understand the meaning of these symbols and interpret logical statements.
Check out my series on building numbers from the ground up:
TIMESTAMPS
00:00 - Intro
03:07 - Or, And, Not
06:28 - Implication
16:39 - Quantifiers
26:26 - Outro
INVESTIGATORS
ftfftttftf is not the slug you are looking for.
CORRECTIONS
*Propositions vs predicates: So that I didn’t overwhelm the viewer I stuck to just using “proposition” throughout. I know this isn’t strictly correct as many of the statements involving variables are actually prediates.
**For some reason when recording I had it in my head that ‘n’ was a British thing when it is widely used throughout the Anglosphere and beyond.
***Slip of the tongue that kind of undermines my point — the converse of Legrange’s Theorem would be “H is a subset with cardiality dividing |G| ⇒ H is a subgroup of G."
****Another slip of the tongue that undermines the point — we are showing that whenever x is NOT zero, it has a reciprocal y=1/x.
CREDITS
All music by Danjel Zambo.
Комментарии
 0:27:32
0:27:32
 0:02:36
0:02:36
 0:06:19
0:06:19
 0:09:33
0:09:33
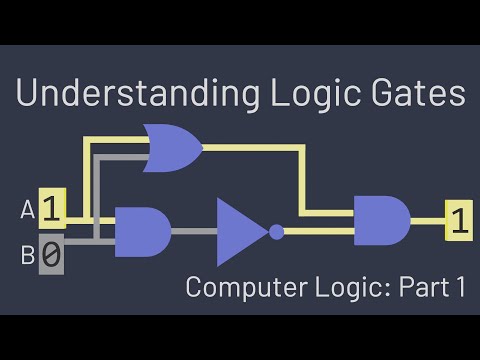 0:07:28
0:07:28
 0:17:58
0:17:58
 0:05:30
0:05:30
 0:07:51
0:07:51
 0:01:00
0:01:00
 0:02:44
0:02:44
 0:05:33
0:05:33
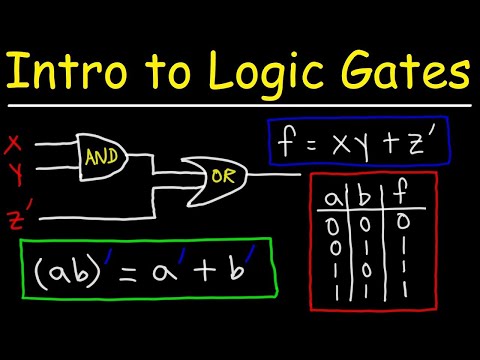 0:54:07
0:54:07
 0:11:20
0:11:20
 0:03:01
0:03:01
 0:06:35
0:06:35
 0:11:24
0:11:24
 0:08:58
0:08:58
 0:05:42
0:05:42
 0:00:23
0:00:23
 0:00:46
0:00:46
 0:07:27
0:07:27
 0:25:22
0:25:22
 0:08:19
0:08:19
 0:08:03
0:08:03