filmov
tv
Convolution Integral: Solving Example and Understanding its Solution | Signals and Systems
Показать описание
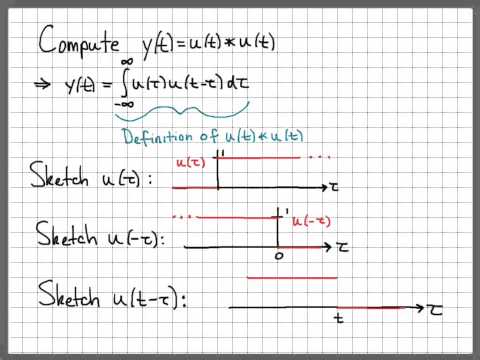
Convolution integral is a mathematical operation that is used to express the relationship between two functions and is often used in signal processing and control systems. The convolution integral is represented by the symbol ∗ (asterisk) and is defined as the integral of the product of one function (f(t)) with a time-reversed and scaled version of another function (g(t)) over the entire range of time. The result of the convolution integral is a third function (h(t)) that describes how the shape of one function is modified by the other function.
The convolution integral is used to model a wide range of systems and processes in various fields such as electrical engineering, physics, and control systems. It is particularly useful in the analysis of linear time-invariant systems, where the output is a convolution of the input and the impulse response of the system. It is also used in signal processing applications such as filtering, image processing, and audio processing.
Solved example of continuous time convolution integral signals and systems is given in this video.
The convolution integral is used to model a wide range of systems and processes in various fields such as electrical engineering, physics, and control systems. It is particularly useful in the analysis of linear time-invariant systems, where the output is a convolution of the input and the impulse response of the system. It is also used in signal processing applications such as filtering, image processing, and audio processing.
Solved example of continuous time convolution integral signals and systems is given in this video.
0:15:56
Convolution integral example - graphical method
0:10:33
The Convolution of Two Functions | Definition & Properties
0:14:02
Convolution in 5 Easy Steps
0:15:10
#112 Solved Problems on Convolution Integral // EC Academy
0:06:00
Convolution Integral: Solving Example and Understanding its Solution | Signals and Systems
0:24:25
Signals and Systems - Convolution theory and example
0:05:15
❖ Convolution of Two Functions ❖
0:06:56
Convolution Integral Example 01 - Convolution of Two Unit Step Functions
0:04:06
#2.10 (b): Solve convolution integral example.
0:04:12
#2.10 (c): Solve convolution integral example.
0:30:42
Introduction to Convolution Operation
0:10:47
Convolution Integral || Graphical Method of Convolution || Example 15.12 || ENA 15.5(1a)(English)
0:03:56
#2.10 (e): Solve convolution integral example.
0:04:01
Example: Convolution Integral
0:09:59
#2.10 (a): Solve convolution integral example.
0:13:42
Convolution by Image Method
0:11:40
Graphical Convolution Integral
0:11:02
Convolution Integral Example 05 - Convolution Of Unit Step With Pulse
0:16:01
Signals & Systems - Convolution of two signals - working examples -1 - UNIT III
0:27:18
Lecture 5 Module 3 Convolution Example Continuous Time
0:13:39
Convolution Integral Example 03 - Convolution of Two Triangles
0:18:35
Continuous Time Convolution || Example 2.6 & 2.7 || S&S 2.2.(1)(English)(Oppenheim)
0:00:55
What is Convolution
0:13:01
Convolution (Solved Problem 1)
Комментарии