The Convolution of Two Functions | Definition & Properties

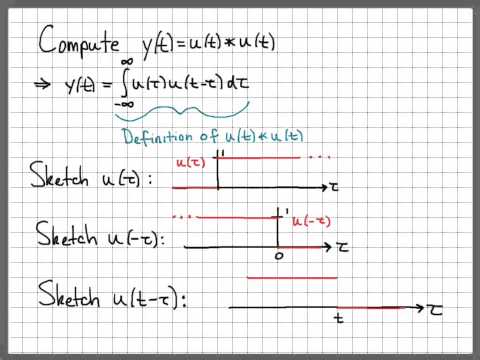
We can add two functions or multiply two functions pointwise. However, the convolution is a new operation on functions, a new way to take two functions and combine them. In this video we define the convolution of two functions, state and prove several of its nice algebraic properties, and see in particular how convolutions play very nicely with Inverse Laplace Transforms and give us way to deal with products. Much like the product rule for derivatives, the formula isn't quite as simple as the product of the inverse laplace transforms, instead it is given by convolutions.

****************************************************
Other Course Playlists:

***************************************************

► Want to learn math effectively? Check out my "Learning Math" Series:

►Want some cool math? Check out my "Cool Math" Series:

****************************************************

*****************************************************

This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.

BECOME A MEMBER:

MATH BOOKS & MERCH I LOVE:

[ejkitchen]

As many others have stated, thank you for making this very easy to understand. It's fascinating how many bad profs there are out there attempting to teach this. If you think about it, it's not that hard but for some reason, many people struggle to explain this properly because they do not spend the time like you did to make it accessible. Again, thank you for doing this.

[vaibhavdlxit]

You turned convolution from a dreaded enemy to an important ally which springs up to rescue while performing inverse laplace of evil looking functions. You sir, are a hero.

[bromarskiii]

You just explained convolution 100 times better than my textbook and my professor! Thanks!!

[migo]

Starting from 10:06 when you starting evaluating the integral & on the second line, the last part should have read: -0.5*TAU*cost t, because your're integrating w.r.t. TAU. Anyways, thanks v. much for all your efforts. God bless!

[ricardobautista-garcia]

Wonderfully explained. Time to do my final exam. Thank you once again.

[eggxecution]

at 10:00 I think you made a mistake in trigo identity, it should be (a-b) also (a+b) to prevent confusion. This identity is product to sum formula if I recall correctly

[josiahkolar]

This playlist and the ODE playlist have been getting me through this 5 week summer class

[RubALamp]

I hope you grow in popularity. Not that it should be needed, but I think many people would benefit from your insight. Thank you for your videos.

[DrDerivative]

if a = tau and b = t - tau, then how did you get b - a = 2tau - t? shouldnt it be t - 2tau?

[sobhanboss]

this came in clutch, you made it so simple while my professor made it super confusing so thank you Trefor

[sarveshchandak]

You cleared up all my confusion. Thanks a lot. ❤️❤️❤️

[ConceptualCalculus]

Just yesterday I was searching for a vid on convolution for my ODE class. Today this new vid popped up in my feed. I'm using it to replace the one I found yesterday, I suppose I should watch this one first, but that's not really necessary. If it is a Trefor Bazett vid, it is good.

[BentHestad]

A quite difficult (but so essential!) concept very well explained! Thanks!

[NPCNo-xmli]

You are single-handedly carrying all my math related subjects throughout my degree.

[PiyushPastor]

Wow. Only if the classes were this good.

[BoZhaoengineering]

Professor Trefor your T shirt is fantastic. Can you please tell me where I can buy one?

[universalalgorithm]

Why do convolutions need to be so convoluted?

[uchiha_kakashi]

so what is the difference between multiplication and convolution

[millionairesclub]

This was so well explained and succinct. Thanks Prof.🙇🏼‍♀️

[jaydean]

Dr Trefor, as usual excellent videos, If there are any math/engineering students that don't "Ace" their exams it is THERE fault...Great JOB !