filmov
tv
Math for fun#15, GEOMETRIC SERIES WANNABE?

Показать описание
Math for fun#15, GEOMETRIC SERIES WANNABE?
blackpenredpen
math for fun,
tags: math for fun has hard math problem, challenging math problems, hard algebra problems, hard calculus problems, sum of b^ln(n), series b^ln(n), hard series problem, calculus 2 series problems, find the values of b so that the series b^ln(n) converges, blackpenredpen, air jordan 11s space jam on feet, jordans 11s space jam, space jam in the background.
blackpenredpen
math for fun,
tags: math for fun has hard math problem, challenging math problems, hard algebra problems, hard calculus problems, sum of b^ln(n), series b^ln(n), hard series problem, calculus 2 series problems, find the values of b so that the series b^ln(n) converges, blackpenredpen, air jordan 11s space jam on feet, jordans 11s space jam, space jam in the background.
Math for fun#15, GEOMETRIC SERIES WANNABE?
Sum of Arithmetic and Geometric sequences - IB Math SL
How REAL Men Integrate Functions
One Geometric Geometric Geometric Geometric ... Series - Papa's Improvised Session #16
5 simple unsolvable equations
Every Student Should See This
9 Math Riddles That'll Stump Even Your Smartest Friends
Infinite sum of powers of 4/9
iShowSpeed BEATS WORLDS HARDEST GEOMETRY DASH LEVEL
Geometry behind the geometric sum of powers of 1/3!
Geometric Series
Math for fun, 1, 2, 3, 4, 5, 8, ____, ____, calculus 2 'find the pattern' for the sequence
HOW TO FIND GEOMETRIC TERMS IN A SEQUENCE AND SUM OF A FINITE GEOMETRIC SERIES || LOVE MATHEMATICS
What does it feel like to invent math?
Geometric Sequence (an interesting piece of math) (1 2 4 8 16 32 64 128)
🔥 POV: Integration - Look at me! 👀 💪 | JEE 2024 | Math | Bhoomika Ma'am
Geometric Shapes
2003 AIME II problem 15 (part 2) | Math for fun and glory | Khan Academy
The Map of Mathematics
Large Numbers
Alternating infinite sum!
Find a Specific Term in a Geometric Sequence
Geometric Series and Everything You Need To Know About Them (Calculus 2)
Infinite Geometric Series
Комментарии
 0:14:05
0:14:05
 0:39:20
0:39:20
 0:00:35
0:00:35
 0:16:42
0:16:42
 0:00:50
0:00:50
 0:00:58
0:00:58
 0:06:40
0:06:40
 0:00:52
0:00:52
 0:00:31
0:00:31
 0:01:00
0:01:00
 0:14:47
0:14:47
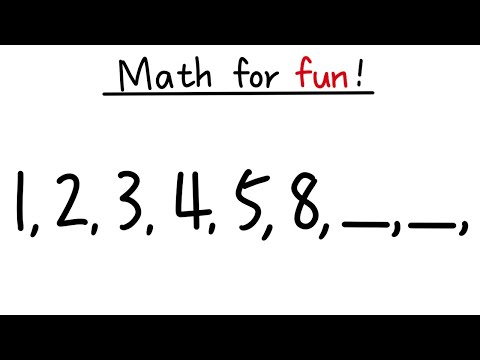 0:04:50
0:04:50
 0:20:56
0:20:56
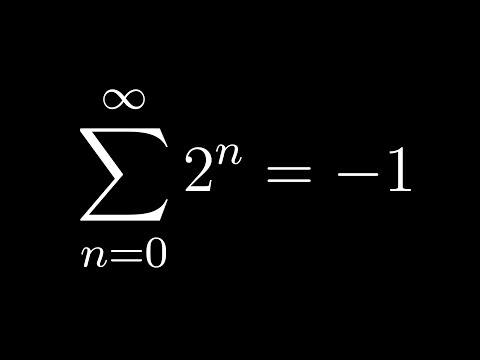 0:15:08
0:15:08
 0:02:43
0:02:43
 0:00:48
0:00:48
 0:00:04
0:00:04
 0:11:34
0:11:34
 0:11:06
0:11:06
 0:00:58
0:00:58
 0:00:52
0:00:52
 0:01:01
0:01:01
 0:29:31
0:29:31
 0:42:05
0:42:05