filmov
tv
Finding local minimum maximum values of a function

Показать описание
This video focuses on how to find the local minimum maximum values of f(x) = 4x^3 - 4x^4. In this video, I show how to use the First Derivative Test to find the local extrema of a function.
The steps for solving the problem are:
1. Find the critical points of f(x).
2. Make a sign chart for f'
3. Classify the critical values using the First Derivative Test.
Your feedback and requests are encouraged and appreciated. Thank you all for watching and please subscribe if you like!
The steps for solving the problem are:
1. Find the critical points of f(x).
2. Make a sign chart for f'
3. Classify the critical values using the First Derivative Test.
Your feedback and requests are encouraged and appreciated. Thank you all for watching and please subscribe if you like!
Finding Local Maximum and Minimum Values of a Function - Relative Extrema
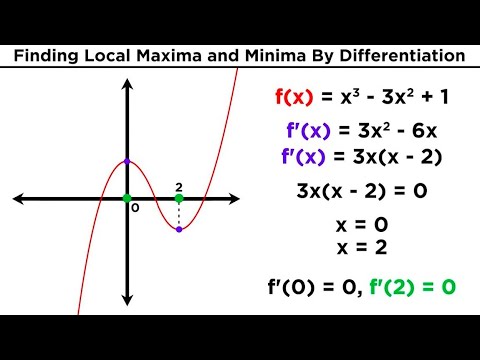
Finding Local Maxima and Minima by Differentiation
📈 Local and Absolute Maximum and Minimum from a Graph 📈
Finding local minimum maximum values of a function
How to Find Local Maximum and Minimum Values of a Polynomial Function | Glass of Numbers
How to Find Local Maximum and Minimum Values of a Rational Function | Calculus | Glass of Numbers
Example: Local Maximum and Minimum Values from a Graph (1)
Determine if a quadratic has a max or min value then find it (mistake)
Maths 2 | Higher order derivatives and Hessian (W11)
Learn how to determine the local max and min from a graph
Finding the Local Maximum/Minimum Values (with Trig Function)
Identifying The Relative Maximum and Minimum Values of a Function
Finding Absolute Maximum and Minimum Values - Absolute Extrema
Learn how to find the absolute max, min and relative max min of a graph
How to find Local Min and Local Max
Local Extrema, Critical Points, & Saddle Points of Multivariable Functions - Calculus 3
Pre-Calculus - Identify the local maximum and minimum of a function
Local Maximum and Local Minimum Values Using First Derivative Test [Just 5 Steps]
Local Maximum and Local Minimum of a Definite Integral Function (Accumulation Function)
Finding local maxima and minima of a function given the graph
Multivariable maxima and minima
Calc 3 Ch.14 Find Local Maxima | Local Minima | Saddle points of the Function | Example #1
How to determine the absolute and local max min of a graph
Find the local maxima or local minima of `f(x) = x^(3) - 6x^(2) + 9x + 15` Also, find the local
Комментарии
 0:14:18
0:14:18
 0:06:17
0:06:17
 0:03:27
0:03:27
 0:08:10
0:08:10
 0:15:36
0:15:36
 0:13:48
0:13:48
 0:02:29
0:02:29
 0:04:54
0:04:54
 1:55:51
1:55:51
 0:04:23
0:04:23
 0:07:42
0:07:42
 0:03:47
0:03:47
 0:17:17
0:17:17
 0:02:41
0:02:41
 0:00:42
0:00:42
 0:14:35
0:14:35
 0:04:57
0:04:57
 0:06:29
0:06:29
 0:03:17
0:03:17
 0:01:58
0:01:58
 0:08:04
0:08:04
 0:05:49
0:05:49
 0:01:26
0:01:26
 0:04:33
0:04:33