filmov
tv
Linear ODEs with Constant Coefficients: Repeated Roots

Показать описание
How to Solve Constant Coefficient Homogeneous Differential Equations
Linear Differential Equation with Constant Coefficients
Higher Order Constant Coefficient Differential Equations: y'''+y'=0 and y'&...
Linear differential equation with constant coefficient
Second Order Linear Differential Equations
Higher Order Homogeneous Differential Equation With Constant Coefficients | Examples Maths
Systems of linear first-order odes | Lecture 39 | Differential Equations for Engineers
BSC Math Lecture: Unit 2 Lecture 06 - ODE Semester 3 Lucknow University #lucknowuniversity #bsc #nep
Higher order homogeneous linear differential equation, using auxiliary equation, sect 4.2#37
Second order homogeneous linear differential equations with constant coefficients
Method of Undetermined Coefficients - Nonhomogeneous 2nd Order Differential Equations
Linear ODEs with Constant Coefficients: Distinct Roots
Homogeneous DE with Constant Coefficients - Auxiliary Equations (Distinct Roots)
Linear differential equation with constant coefficient || Methods for C.F
Linear ODEs with Constant Coefficients: Matching the Initial Conditions
How to Solve First Order Linear Differential Equations
Undetermined Coefficients: Solving non-homogeneous ODEs
First Order Linear Differential Equations
(2.2) Solve 2nd Order Linear Homogeneous ODEs with Constant Coefficients
🔵18 - Second Order Linear Homogeneous Differential Equations with Constants coefficients
Constant Coefficient ODEs: Real & Distinct vs Real & Repeated vs Complex Pair
Session 19: Second order Homogeneous Linear differential equation with constant coefficients!!
Linear Higher Order Differential Equation | CF & PI |Lecture-I
Linear Differential Equation with Constant Coefficient of Higher Order|One Shot|Pradeep Giri Sir
Комментарии
 0:06:41
0:06:41
 0:18:36
0:18:36
 0:11:19
0:11:19
 0:22:43
0:22:43
 0:25:17
0:25:17
 0:10:04
0:10:04
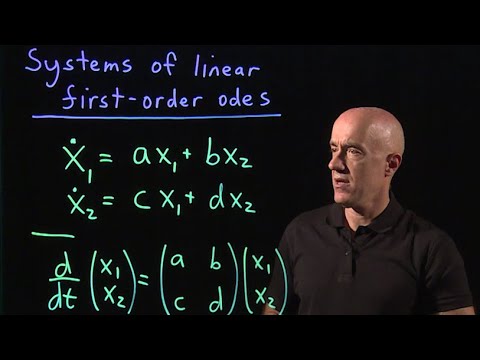 0:08:28
0:08:28
 0:38:48
0:38:48
 0:11:03
0:11:03
 0:11:44
0:11:44
 0:41:28
0:41:28
 0:17:06
0:17:06
 0:35:55
0:35:55
 0:30:45
0:30:45
 0:04:03
0:04:03
 0:10:53
0:10:53
 0:12:44
0:12:44
 0:22:28
0:22:28
 0:08:24
0:08:24
 0:26:57
0:26:57
 0:11:50
0:11:50
 0:14:06
0:14:06
 0:33:59
0:33:59
 0:34:57
0:34:57