filmov
tv
What is 2^π?
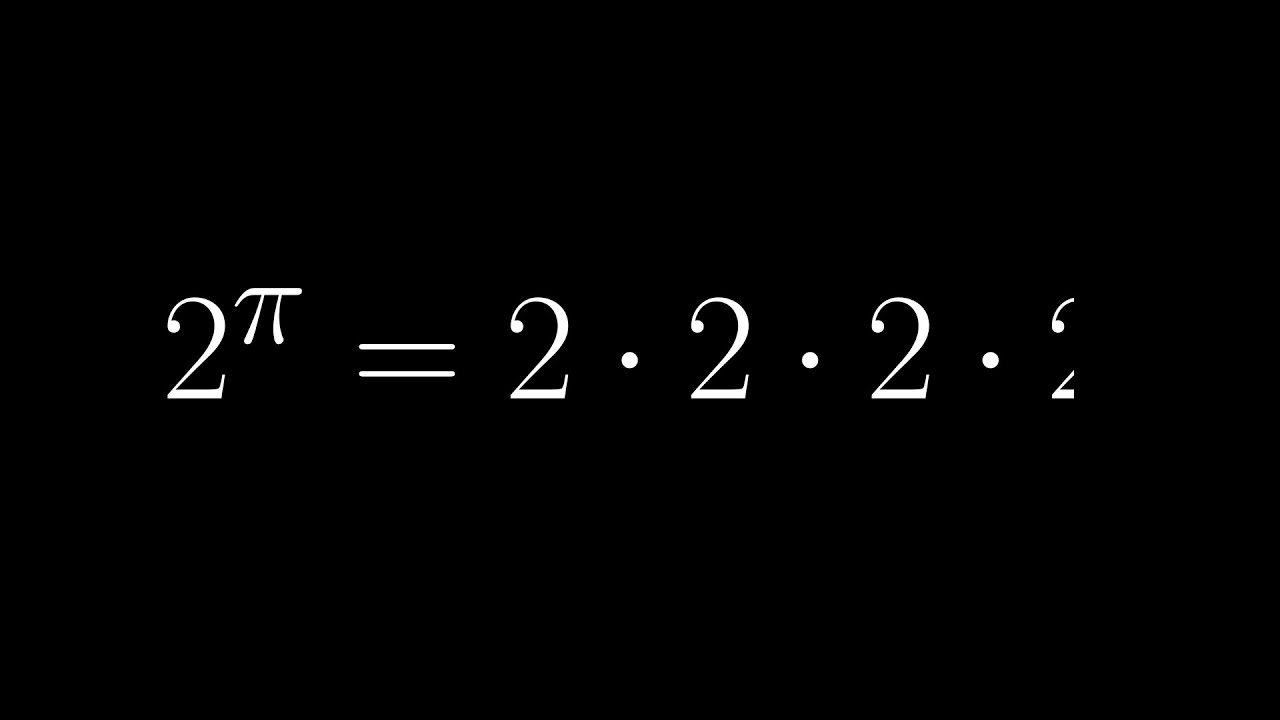
Показать описание
Figuring out what 2^π means
Resources on exponentiation:
Resources about the exponent algorithms:
Corrections:
Resources on exponentiation:
Resources about the exponent algorithms:
Corrections:
Why does 2π = 360° ?
Why is π = 3.14…??? #pivalue #circle #circles #geometry #maths #mathematics
Math Antics - Circles, What Is PI?
Why is pi here? And why is it squared? A geometric answer to the Basel problem
Does π make sense?
What Is The Factorial Of 1/2? SURPRISING (1/2)! = (√π)/2
Memory Trick | Easiest way to remember pi
exact value of pi | value of pi in math | what is the value of pi | what is pi | #shorts
Lindas Estradas do Piauí, Parte 2 Trecho entre PortoPI /Miguel Alves-PI #estrada #nordeste
Number Pi - π - Math for Kids - What is Number Pi?
Why π is in the normal distribution (beyond integral tricks)
Trigonometric Values 0, π/2, π, 3π/2, 2π,⋅⋅⋅ at Lightning Speed
The Pi Song (Memorize 100 Digits Of π) | SCIENCE SONGS
Permute Pi To Make Phi
Was ist Pi? | ALMANIA
What is (-1)^π equal to?
The (Nearly) Perfect Pi Approximation #shorts
The Pi Alphabet Clock #shorts
Why Pi is Approximately 22/7 | EN
Tau vs Pi Smackdown - Numberphile
What is Pi? | Circles | Circumference | Don't Memorise
Ramanujan's Magnificent Formula For π #ramanujan #mathematics #maths
Compute sin(pi/2)
How did Newton Calculate Pi? #shorts
Комментарии
 0:00:27
0:00:27
 0:00:31
0:00:31
 0:07:58
0:07:58
 0:17:08
0:17:08
 0:00:57
0:00:57
 0:04:55
0:04:55
 0:00:19
0:00:19
 0:00:25
0:00:25
 0:00:51
0:00:51
 0:03:52
0:03:52
 0:24:46
0:24:46
 0:06:06
0:06:06
 0:01:15
0:01:15
 0:00:44
0:00:44
 0:00:45
0:00:45
 0:02:31
0:02:31
 0:00:58
0:00:58
 0:00:41
0:00:41
 0:01:41
0:01:41
 0:11:12
0:11:12
 0:04:45
0:04:45
 0:00:37
0:00:37
 0:01:00
0:01:00
 0:00:54
0:00:54