Permute Pi To Make Phi

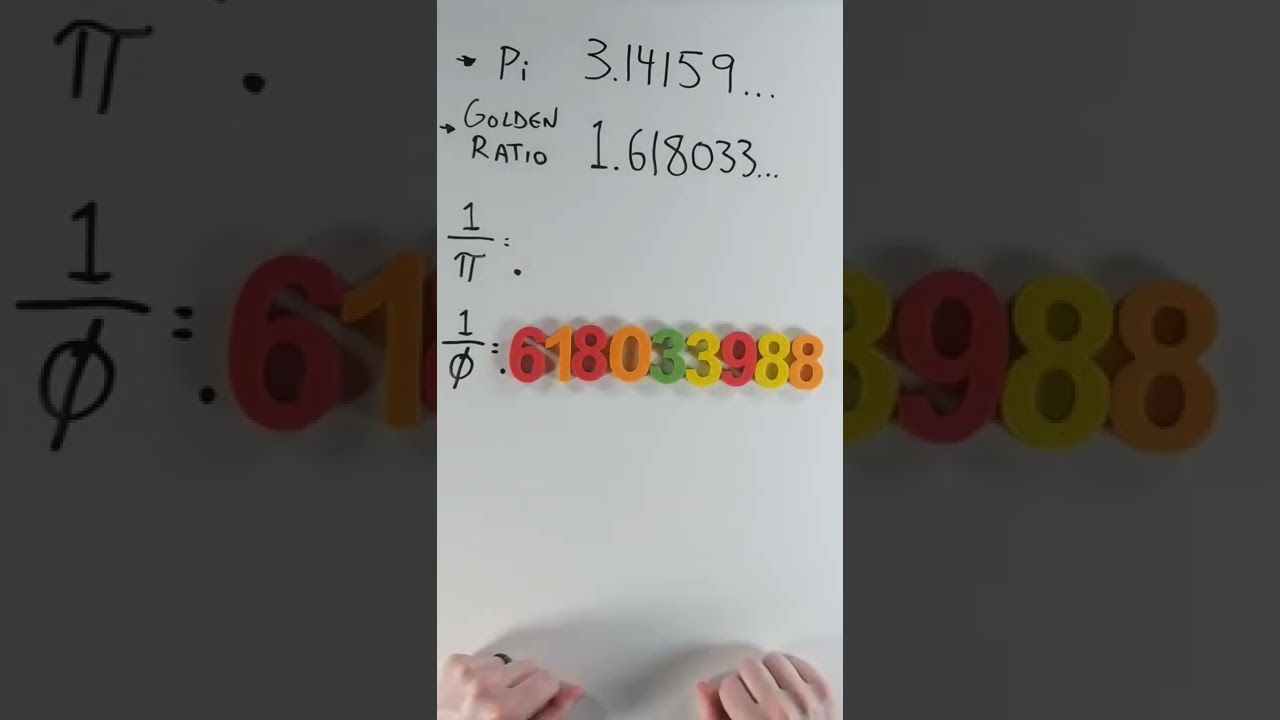
Показать описание

There are only a handful of truly legendary numbers, like 0, 1, and Euler's Number. And there are only 10 digits from 0-9, so it would make sense that we can shift them around to see some interesting things... right?

Sometimes it feels like too much of a coincidence, like being able to take the reciprocal of Pi and permute its digits into the reciprocal of the Golden Ratio. Not enough for you? Tack on another Pi digit and throw it in front of the reciprocal of Phi and you'll get the actual Golden Ratio's digits.

HOW CAN THIS BE A COINCIDENCE?!

#math #mathematics #vsauce

Рекомендации по теме

Комментарии

THis feels to me like the BIble code - if you mess around with enough numbers long enough, you're bound to get some coincidences, and these are not even all that strong coincidences.

Martial-Mat

If you choose some digits of pi and permute them, you can get any number.

YSPACElabs

The first part was kinda cool.
The second part was just the definition of φ, which is φ = 1/φ + 1

DeJay

“Is it just coincidence?”
More likely than not, yes. Many a mathematician has been absorbed in the sea of coincidences and had nothing to show for it

ozzi

e has some cool coincidences as well

2.7, then 1828, then 1828 again, then 45 90 45 (the degrees in an isosceles right triangle), then 235 ( the first three primes), then 360 (the number of degrees in a circle).

So all together it looks like:
2.718281828459045235360

Makes it super easy to remember

axbs

Oh wow, two arbitrary numbers in an arbitrary number system have the same digits. Of course it's a coincidence, come on...

SwordQuake

It's a whole lot easier to do if you always work in base 2.

CrashSable

Conspiracy theorist: Gonna take that as an Evidence Aliens.

maxchronos

You think that's crazy? Just wait until you take all infinity digits of pi and permute them to get all infinity digits of phi.

ajreukgjdi

Great job! I hadn’t ever thought about that. Thank you for giving me something interesting to think about.👍

supermegageek

I mean the fact you can choose 9 gives it a pretty high statistical probability of existing. In fact, the chance that you could not find two famous irrational numbers that this occurs with is about 0.002472% if I did my math right.

TheNoerdy

Wow. Who numbers with non finite decimal places have some digits in common. How would have thought?

cubeheadgameing

Wait there's more... 1/phi = phi - 1

Here's something weird about Phi that I noticed, the more times you multiply it by itself the closer the result gets to a whole number. It will be long decimal numbers, the decimals getting more and more nines or zeros after the decimal point with each multiplication, one answer will start with nines after the decimal and the next will start with zeroes. It only works with the real Phi as produced in a calculator, not a shortened version. Maybe that's why Phi is found so often in nature in things that get gradually larger. Maybe that's the lowest number after one that can do that. You could do it with two but nature would only go as high as necessary, for efficiency. Why go to 2 x 2 etc when you could get a similar outcome of almost whole numbers starting with less than 2? A possible glitch with this is that it only gets to nines or zeroes after the decimal after the first four multiplications, the first 3 are still far from whole numbers. How would a sunflower make 3 partial number of seeds before the whole ones? It would have to round off I guess.

aliengrey