filmov
tv
What is the area? A nice problem from Singapore
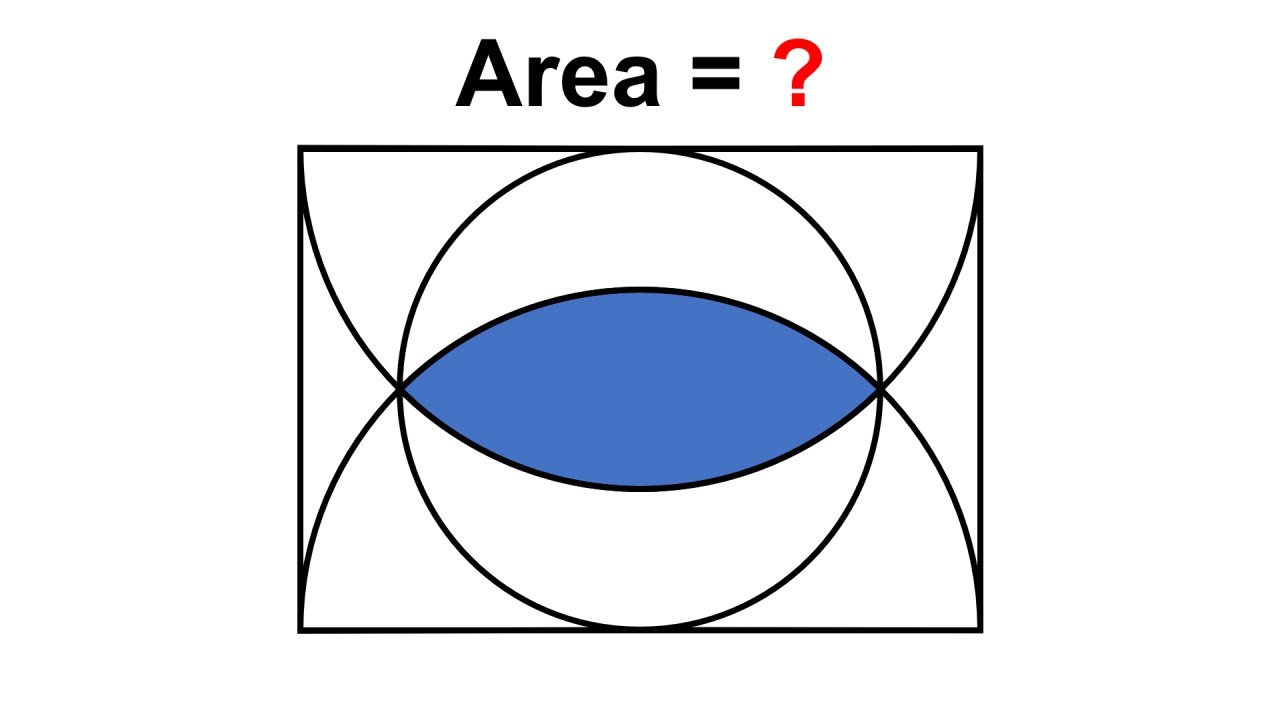
Показать описание
Can you solve this challenging problem from the Mathematical Olympiad of Singapore? Thanks to Truong from Vietnam for the suggestion!
Send me suggestions by email (address in video). I cannot reply to everyone but I consider all ideas!
Like many YouTubers I use popular software to prepare my videos. You can search for animation software tutorials on YouTube to learn how to make videos. Be prepared--animation is time consuming and software can be expensive!
Why are there comments before the video is published? Get early access and support the channel on Patreon
If you buy from the links below I may receive a commission for sales. (As an Amazon Associate I earn from qualifying purchases.) This has no effect on the price for you.
Show your support! Get a mug, a t-shirt, and more at Teespring, the official site for Mind Your Decisions merchandise:
My Books (worldwide links)
My Books (US links)
Mind Your Decisions: Five Book Compilation
A collection of 5 books:
"The Joy of Game Theory" rated 4.2/5 stars on 141 reviews
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" rated 3.7/5 stars on 11 reviews
"40 Paradoxes in Logic, Probability, and Game Theory" rated 4/5 stars on 23 reviews
"The Best Mental Math Tricks" rated 4.4/5 stars on 38 reviews
"Multiply Numbers By Drawing Lines" rated 4.5/5 stars on 19 reviews
Mind Your Puzzles: Collection Of Volumes 1 To 3
A collection of 3 books:
"Math Puzzles Volume 1" rated 4.6/5 stars on 40 reviews
"Math Puzzles Volume 2" rated 4.5/5 stars on 14 reviews
"Math Puzzles Volume 3" rated 4.6/5 stars on 12 reviews
Connect with me
2017 Shorty Awards Nominee. Mind Your Decisions was nominated in the STEM category (Science, Technology, Engineering, and Math) along with eventual winner Bill Nye; finalists Adam Savage, Dr. Sandra Lee, Simone Giertz, Tim Peake, Unbox Therapy; and other nominees Elon Musk, Gizmoslip, Hope Jahren, Life Noggin, and Nerdwriter.
Press
Send me suggestions by email (address in video). I cannot reply to everyone but I consider all ideas!
Like many YouTubers I use popular software to prepare my videos. You can search for animation software tutorials on YouTube to learn how to make videos. Be prepared--animation is time consuming and software can be expensive!
Why are there comments before the video is published? Get early access and support the channel on Patreon
If you buy from the links below I may receive a commission for sales. (As an Amazon Associate I earn from qualifying purchases.) This has no effect on the price for you.
Show your support! Get a mug, a t-shirt, and more at Teespring, the official site for Mind Your Decisions merchandise:
My Books (worldwide links)
My Books (US links)
Mind Your Decisions: Five Book Compilation
A collection of 5 books:
"The Joy of Game Theory" rated 4.2/5 stars on 141 reviews
"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" rated 3.7/5 stars on 11 reviews
"40 Paradoxes in Logic, Probability, and Game Theory" rated 4/5 stars on 23 reviews
"The Best Mental Math Tricks" rated 4.4/5 stars on 38 reviews
"Multiply Numbers By Drawing Lines" rated 4.5/5 stars on 19 reviews
Mind Your Puzzles: Collection Of Volumes 1 To 3
A collection of 3 books:
"Math Puzzles Volume 1" rated 4.6/5 stars on 40 reviews
"Math Puzzles Volume 2" rated 4.5/5 stars on 14 reviews
"Math Puzzles Volume 3" rated 4.6/5 stars on 12 reviews
Connect with me
2017 Shorty Awards Nominee. Mind Your Decisions was nominated in the STEM category (Science, Technology, Engineering, and Math) along with eventual winner Bill Nye; finalists Adam Savage, Dr. Sandra Lee, Simone Giertz, Tim Peake, Unbox Therapy; and other nominees Elon Musk, Gizmoslip, Hope Jahren, Life Noggin, and Nerdwriter.
Press
Комментарии
 0:04:27
0:04:27
 0:33:51
0:33:51
 0:03:15
0:03:15
 0:06:31
0:06:31
 0:05:55
0:05:55
 0:08:18
0:08:18
 0:04:26
0:04:26
 0:02:48
0:02:48
 0:04:34
0:04:34
 0:02:25
0:02:25
 0:04:01
0:04:01
 0:05:49
0:05:49
 0:04:11
0:04:11
 0:07:58
0:07:58
 0:03:48
0:03:48
 0:03:08
0:03:08
 0:02:44
0:02:44
 0:02:43
0:02:43
 0:04:34
0:04:34
 0:03:52
0:03:52
 0:07:09
0:07:09
 0:02:51
0:02:51
 0:04:13
0:04:13
 0:27:14
0:27:14