filmov
tv
Solving a tricky SAT square root problem

Показать описание
How do we combine square root numbers? Here we will work out the square root of 20 minus the square root of 5, i.e. sqrt(20)-sqrt(5)=? You need to know how to simplify square root numbers and how to combine square root numbers for your algebra class! Subscribe to @bprpmathbasics for more algebra tutorials.
0:00 sqrt(20)-sqrt(5)=?
4:21 You try sqrt(18)-sqrt(8)=?
-----------------------------
-----------------------------
#math #algebra #mathbasics
0:00 sqrt(20)-sqrt(5)=?
4:21 You try sqrt(18)-sqrt(8)=?
-----------------------------
-----------------------------
#math #algebra #mathbasics
Solving a tricky SAT square root problem
A tricky SAT square Root question
Solve SAT square root tricky question.
Solving a tricky sum of square roots (Olympiad practice)
Solve by completing the square | Step by Step Technique
Solve by Completing the Square: Step-by-Step Technique
the 'SAT way' to complete the square (and also the regular way)
How To Complete The Square | Math Tips To Use On The SAT & ACT
SAT Prep||unit 4||Evaluate functions||Composite functions||isolating quantities||quadratic systems
October SAT Prediction: Tricky Conversions with Square Units!
SAT Math | Solving Square Roots Equations
SAT® Math: Square Roots #shorts
SAT Equation of a Circle Problem (Completing the Square)
common SAT square root equation
2 Circles 1 Square
Tricky College Entrance Question | How to Solve Square Root problem in 5 seconds | Olympiad Math
**MASTER** SAT® / ACT® Completing the Square Questions
Square Root Strategies for your ACT SAT Test
Converting Square Units on the SAT
Completing the Square to Solve a Circle SAT
Hexagon Area relation with square of side NEW SAT Practice Test 1
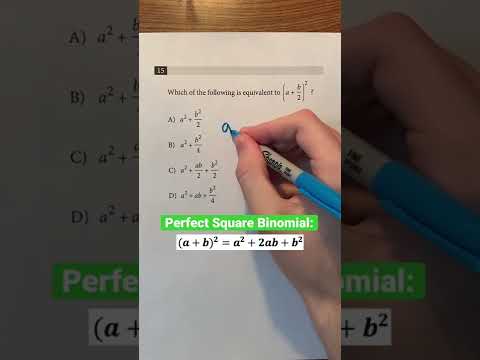
Perfect Square Binomials On The SAT #Shorts #math #maths #mathematics #SAT #ACT #exam #test #learn
SAT Math | Solving Equation with Square Roots
LET, UPCAT, SAT, MCQ REVIEW - solving equation with square roots #shorts
Комментарии
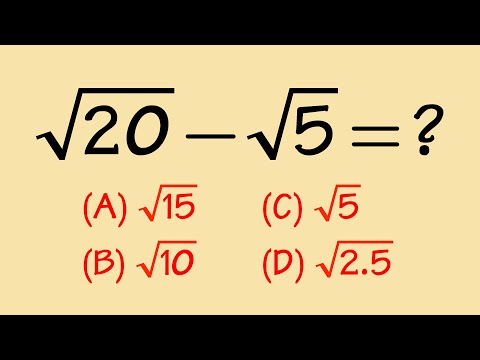 0:04:33
0:04:33
 0:06:47
0:06:47
 0:02:21
0:02:21
 0:05:25
0:05:25
 0:05:20
0:05:20
 0:07:40
0:07:40
 0:04:15
0:04:15
 0:08:14
0:08:14
 0:58:29
0:58:29
 0:00:36
0:00:36
 0:05:31
0:05:31
 0:00:35
0:00:35
 0:03:05
0:03:05
 0:01:40
0:01:40
 0:03:35
0:03:35
 0:02:48
0:02:48
 0:11:38
0:11:38
 0:00:59
0:00:59
 0:00:59
0:00:59
 0:02:59
0:02:59
 0:06:57
0:06:57
 0:00:37
0:00:37
 0:05:31
0:05:31
 0:00:59
0:00:59