filmov
tv
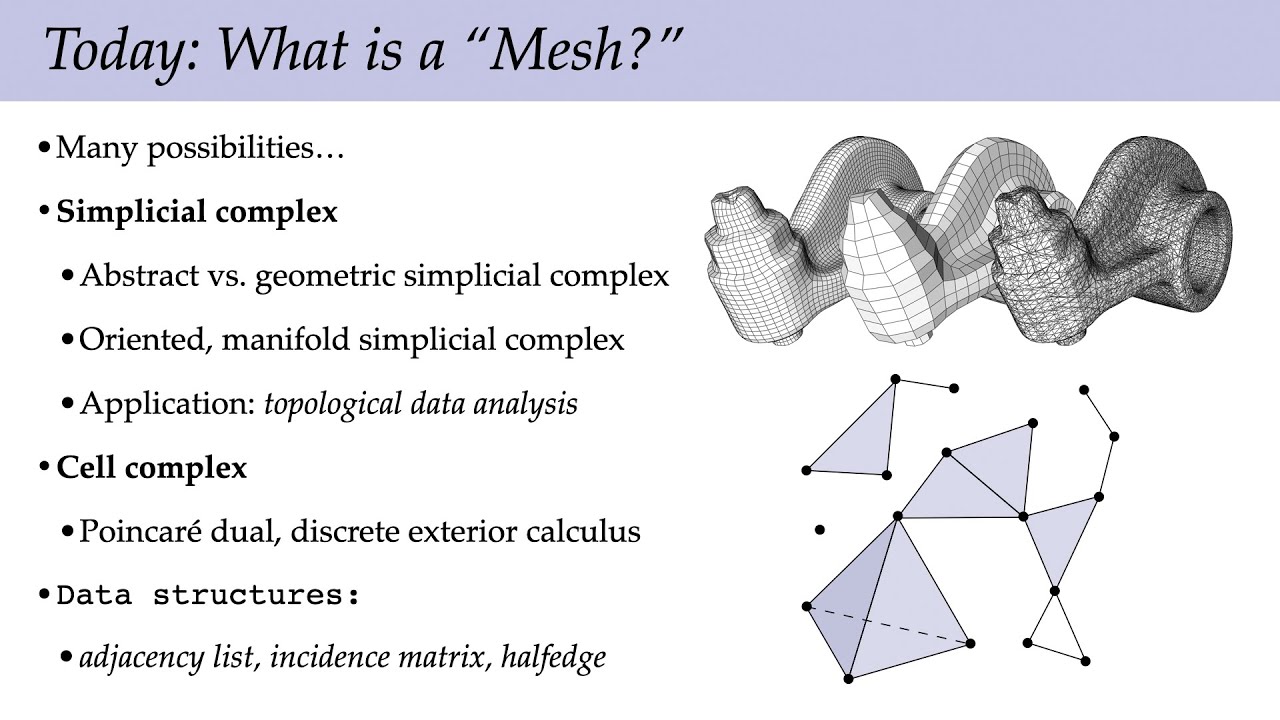
Lecture 2A: What is a 'Mesh?' (Discrete Differential Geometry)
Показать описание
Lecture 2A: What is a 'Mesh?' (Discrete Differential Geometry)
Lecture 2A Introduction to Construction Management: The Role of Project Management in Construction
Lecture 2a: Introduction to Innate Immunity
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Mathematik 1 (lecture 2A) - Rechenregeln und Brüche
My Response to President Obama's Lecture to Black Men
Linear Algebra II: Oxford Mathematics 1st Year Student Lecture - James Maynard
Math 2A. Calculus. Lecture 01. Functions.
Digital Design & Computer Arch. - Lecture 2a: Course Goals & Logistics (ETH Zürich, Spring 2...
Lecture 2 - Team and Execution (Sam Altman)
Lecture 2: From Soviet Communism to Russian Gangster Capitalism
NWC INS Lecture Series -- Lecture 2 'Who Lost the Vietnam War?'
Vehicle Dynamics Lecture #2a: basic terms, steering, tires, roll center
Lecture-2A (Vectors)
💖 IIT Delhi Lecture Hall Actual View 🥰 IITJEE 💥 Best Motivation for JEE Aspirants 🔥JEE Mains #shorts...
Lecture 2: Introduction and Overview II
Cosa significa 'I see'? Scoprilo in questo video! #inglese #englishschool #ingleseperitali...
Lecture 2a: Ẹdo Subject Pronouns | I, You, He, She, It, We, They
Lecture 11 - Hiring and Culture, Part 2 (Patrick and John Collison, Ben Silbermann)
Math 2A. Calculus. Lecture 19. Compound Interest.
Tet ctet tait Psychology notes 2024 | Child psychology tet 2024 | CDP # mahatet2024 #shorts #trend
Classical Mechanics | Lecture 2
iOS Application Development - WiSe 18/19 Lecture 2a: Seminar Topics
mechanism of action of colchicine #pharmacology #gout #colchicine #autacoidpharmacology
Комментарии
 0:58:03
0:58:03
 0:45:21
0:45:21
 0:30:45
0:30:45
 0:00:12
0:00:12
 0:19:25
0:19:25
 0:06:47
0:06:47
 0:53:55
0:53:55
 0:51:03
0:51:03
 0:23:23
0:23:23
 0:46:19
0:46:19
 1:10:43
1:10:43
 0:58:01
0:58:01
 0:37:41
0:37:41
 0:14:00
0:14:00
 0:00:59
0:00:59
 1:14:38
1:14:38
 0:00:42
0:00:42
 0:14:21
0:14:21
 0:50:37
0:50:37
 0:43:20
0:43:20
 0:00:17
0:00:17
 1:39:04
1:39:04
 0:18:12
0:18:12
 0:00:26
0:00:26