filmov
tv
Evaluate the sum of two angles with cosine

Показать описание
👉 Learn how to evaluate the cosine of an angle in radians using the sum/difference formulas. To do this, we first express the given angle as a sum or a difference of two (easy to evaluate) angles, then we use the unit circle and the Pythagoras theorem to identify the angles and obtain all the needed trigonometric function values of the angles. When we know the trigonometric function values of the two angles to be added or subtracted, we can apply the sum and difference formulas to evaluate the cosine of the given angle.
Organized Videos:
✅ Sum and Difference Formulas
✅ Evaluate Sum and Difference Formulas from a Triangle
✅ Simplify an Expression using Sum and Difference Formulas
✅ Write the Expression as a single function | Sum and Difference Formulas
✅ Verify Identities using Sum and Difference Identities
✅ Evaluate Tangent using Sum and Difference Formulas
✅ Evaluate Cosine using Sum and Difference Formulas
✅ Evaluate Sine using Sum and Difference of Two Angles
✅ Solve Equations using Sum and Difference Formulas
Connect with me:
#analytictrig #brianmlogan
Organized Videos:
✅ Sum and Difference Formulas
✅ Evaluate Sum and Difference Formulas from a Triangle
✅ Simplify an Expression using Sum and Difference Formulas
✅ Write the Expression as a single function | Sum and Difference Formulas
✅ Verify Identities using Sum and Difference Identities
✅ Evaluate Tangent using Sum and Difference Formulas
✅ Evaluate Cosine using Sum and Difference Formulas
✅ Evaluate Sine using Sum and Difference of Two Angles
✅ Solve Equations using Sum and Difference Formulas
Connect with me:
#analytictrig #brianmlogan
How to evaluate the sum of two functions
What is the sum of 3/4 and 2/3?
Evaluate the sum of two angles using tangent
Evaluate the sum of two angles with cosine
Summation Formulas and Sigma Notation - Calculus
Learn how to evaluate the sum of two angles with tangent
How to evaluate sum of two angles using the sum formula for sine
How To Find The Sum of an Arithmetic Series - Algebra
Evaluate an expression using the sum and difference of two angles
Find the Sum of the Series SUM((2^n + 1)/3^n)
Finding the sum or an arithmetic series using summation notation
Finding The Sum of an Infinite Geometric Series
Learning to evaluate the sum of two angles in radians, tan
Evaluate the sum of two angles using the tangent formula, tan
Excel SUM and SUMIF Formula in Excel
How to evaluate using the sum of two angles for sine
Evaluate the sum difference identities of two triangles
Sum of n/2^n
Pre-Calculus - Evaluating the Sum of Two Logarithms
Infinite Geometric Series Sum
Sigma Notation and Summation Notation
Math tutorial for determining the sum of an arithmetic series
Let's Evaluate A Sum of Two Cube Roots
Draw a flowchart to find the sum of two numbers
Комментарии
 0:01:10
0:01:10
 0:03:05
0:03:05
 0:03:18
0:03:18
 0:04:46
0:04:46
 0:20:24
0:20:24
 0:05:44
0:05:44
 0:02:58
0:02:58
 0:10:38
0:10:38
 0:01:05
0:01:05
 0:03:57
0:03:57
 0:03:53
0:03:53
 0:19:50
0:19:50
 0:09:36
0:09:36
 0:04:31
0:04:31
 0:07:53
0:07:53
 0:05:37
0:05:37
 0:05:37
0:05:37
 0:06:42
0:06:42
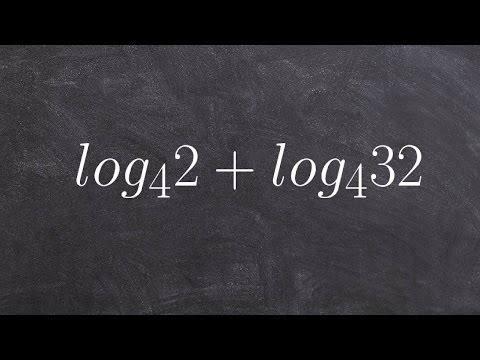 0:01:51
0:01:51
 0:00:45
0:00:45
 0:15:41
0:15:41
 0:06:37
0:06:37
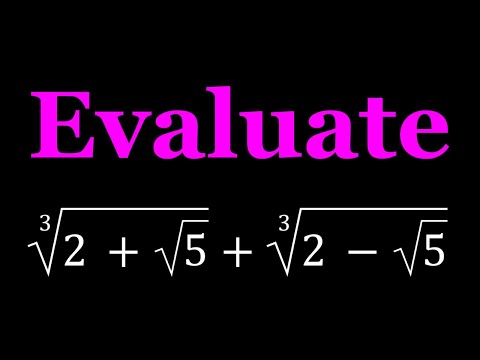 0:09:14
0:09:14
 0:00:58
0:00:58