filmov
tv
Integral of x^i

Показать описание
Learn how the complex integral of x^i can help us find the integral of sin(ln(x)) and cos(ln(x)) without using integration by parts. Complexifying the integral is an integration technique that is usually not taught in calculus 2.
Subscribe to @blackpenredpen for more fun math videos.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Subscribe to @blackpenredpen for more fun math videos.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
DEFINITE INTEGRAL
Integrating x^x
Integral of abs(x) in 44 seconds!
integration by parts is easy
How to solve the Integral of xdx?
This is all Integration is (quickfire AI lesson)
integral of e^sqrt(x), integration by parts in the u-world
How REAL Men Integrate Functions
Can YOU find the integral of tan^-1 { ax/(x(1+x^2)) } from 0 to infinity in 30 minutes?
Integral of absolute value of x or abs(x)
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Integral of e^sqrt(x)
integral of x^x vs integral of x^ln(x) (aren't they both impossible?)
integral of sin(x^2) haunts me
integral of csc(x), the standard result, calculus 2 tutorial
Differentiation and integration important formulas||integration formula
Integral ln(x)
Integral of x squared
The Bernoulli Integral is ridiculous
Integral of e^x/x vs. integral of 1/ln(x)
Differentiation and Integration formula
The *Complex* Integral of (-1)^x
Integral of 1/x
Integral of ln(x) fast!
Комментарии
 0:20:19
0:20:19
 0:00:29
0:00:29
 0:00:44
0:00:44
 0:00:33
0:00:33
 0:00:52
0:00:52
 0:00:59
0:00:59
 0:04:10
0:04:10
 0:00:35
0:00:35
 0:07:31
0:07:31
 0:01:59
0:01:59
 0:00:09
0:00:09
 0:05:43
0:05:43
 0:08:50
0:08:50
 0:00:17
0:00:17
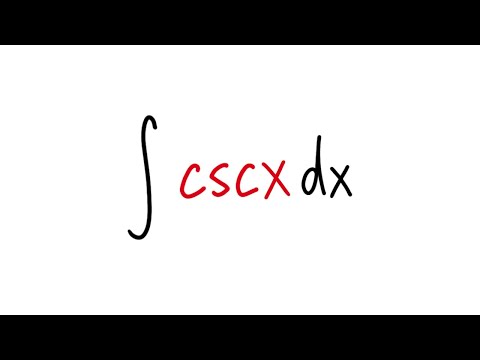 0:03:46
0:03:46
 0:00:16
0:00:16
 0:00:24
0:00:24
 0:00:42
0:00:42
 0:10:00
0:10:00
 0:08:48
0:08:48
 0:00:06
0:00:06
 0:00:51
0:00:51
 0:00:50
0:00:50
 0:00:45
0:00:45