filmov
tv
Integral of abs(x) in 44 seconds!

Показать описание
[Learn Calculus FAST] Check out the following playlists
[More Fun Stuff]
#shorts
bprp fast
Integral of abs(x) in 44 seconds!
Integral of absolute of x or abs (x)
What is the Integral of abs(x)
Definite Integral with Absolute Value |2x - 7| from 0 to 7/2
Integral of abs(x) using integration by parts
How to evaluate the definite integral with absolute value
Definite Integral of the Absolute Value of x from -1 to 2
Integral of absolute value of x (abs x)
Definite Integral with Absolute Value (Example)
Absolute value integral
Integral of abs x | #Shorts #absx #integral #mathematics #maths
Integration of 4/x || 4/x integration || Integral of 4/x
Definite Integral with Absolute Value
integral of absolute value of x
Definite Integral of Absolute Function
Setting Up Definite Integral of Absolute Value Function
Definite Absolute Value Integral
Solving an integral of an integral
How to Evaluate the Definite Integral with Absolute Value
The TRUE Integral of |x|, the absolute value. | Shorts
2016 Maths 2u HSC Q9 Evaluate integral of absolute value function y=|x+1| from x=-3 to 2
Integration of Absolute Value Functions Made Easy
How to Find the Definite Integral of an Absolute Value Function Ex #1
Evaluate the Integral of the Absolute Value of x from -1 to 2 using a Familiar Area Formula
Комментарии
 0:00:44
0:00:44
 0:05:33
0:05:33
 0:05:05
0:05:05
 0:04:44
0:04:44
 0:05:09
0:05:09
 0:04:33
0:04:33
 0:03:02
0:03:02
 0:02:19
0:02:19
 0:07:17
0:07:17
 0:16:09
0:16:09
 0:00:30
0:00:30
 0:01:17
0:01:17
 0:08:25
0:08:25
 0:00:23
0:00:23
 0:00:18
0:00:18
 0:03:06
0:03:06
 0:07:40
0:07:40
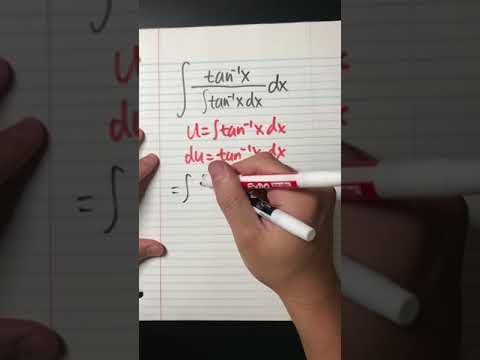 0:00:44
0:00:44
 0:08:23
0:08:23
 0:01:00
0:01:00
 0:01:30
0:01:30
 0:25:34
0:25:34
 0:06:41
0:06:41
 0:04:15
0:04:15