The Cross Product and the Exceptional G2

Summary:

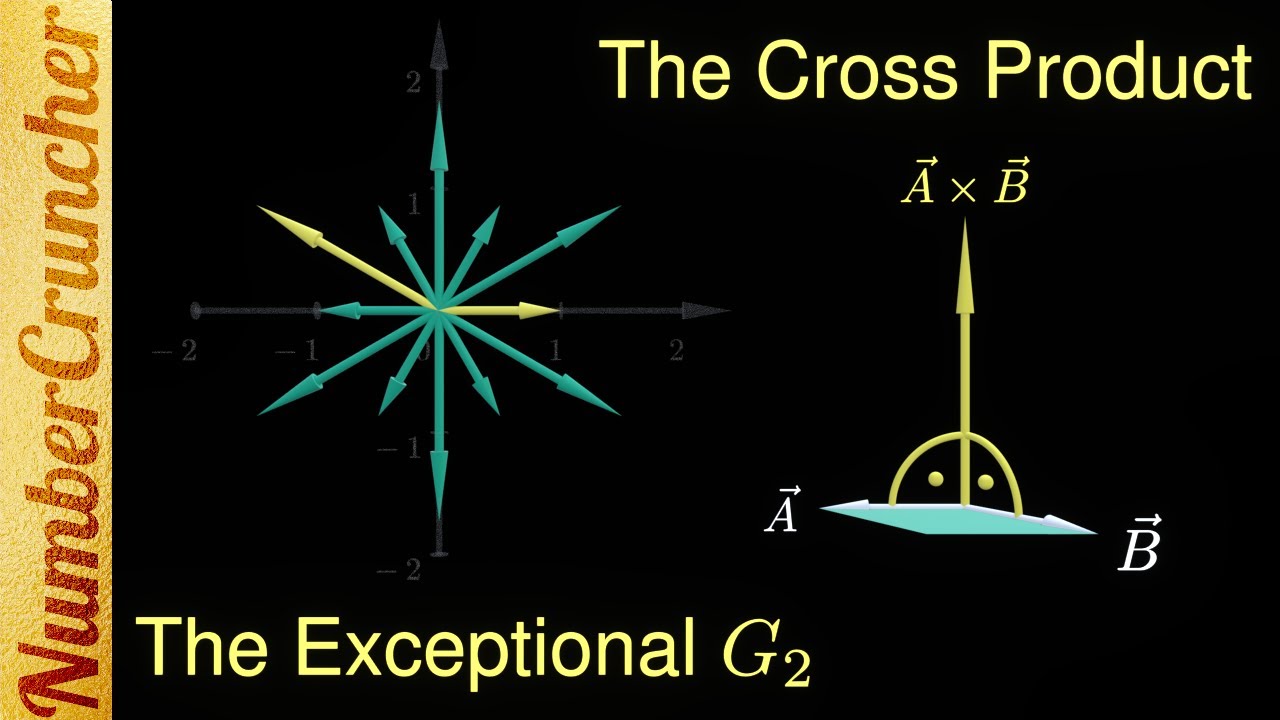
This video shows the connection between the cross product in seven dimensions to the exceptional Lie group G2. The red line through the video is provided by the transformation properties of vectors under changes of the coordinate system.

The G2 is discovered accidentally as a subgroup of SO(7) that preserves the transformation properties of the cross product in 7D.

For further readings we recommend the community post:
where more details are presented for the various Lie algebras, the octonions and the connection between the octonions, the cross product and the exceptional Lie group G2.

Here is the link to an amazing lecture by Micheal Penn on the cross product in various dimensions:

Content:
0:00 introduction
2:45 branding
4:30 rotations in 3D
6:43 the cross product in 3D
9:06 the cross product in 7D
10:44 rotations in 7D
11:46 the disappointment
13:25 the restoration and the the G2 discovery
14:50 sneak preview
16:15 g2 in a nutshell
17:13 the computation of the root lattices
19:25 outro and references

References:

The presented notebook can be downloaded from here:

[SultanLaxeby]

This interpretation of the generators of G2 as infinitesimal rotations in two simultaneous planes is really cool! This gives an intuitive reason why the rank of G2 is two: because in a 7-dimensional space, you can have at most 3 orthogonal planes, which gives you at most two such commuting generators: one rotating planes 1 and 2, the other in plane 2 and 3 for example.

[jakobthomsen]

Cool to learn about the connection between G2 and SO(7) :-)

[Milan_Openfeint]

From 12:40 on, it would have to go like 3x slower for me to be able to follow.
Why did you pick the 7th dimension to check? Does each dimension have its own restoration? Why are there 14 combinations? How does R14 restore both R36 and R27?
How did you pick the signs of a_i b_j in AxB?
How did you even arrive at AxB? Why are the first 3 dimensions different in that the cross product of 3D vectors stays in the first 3 dimensions, but other cross products have non-zero components in the first 3? Questions, questions...

[danielprovder]

what does this 7d cross product have in common with the Freudenthal Square?

[ariaden]

The 3D vector multiplies two polar vectors into an axial vector, which is a bivector in disguise. I wonder what "real" structure is the 7D cross product result.
Alternatively, the 3D vector product can be defined using the contravariant Levi-Civita tensor. The 7D cross product should be definable in a similar way, its tensor probably having something to do with octonions.

[smolboi]

I have 2 different flavours of vectors as a concept in my brain. There is the Physics one where they are independent of choice of coordinates and coordinates must transform opposite to how the axes transform. Then there is the Math one where a vector is anything that satifies the 10 axioms are vectors in a linear space. So stuff like polynomials and functions are vectors. I wonder if we should name them differently or are they actually the same thing cause these 2 concepts sound very different to me.

[purplenanite]

How did the 7D cross product come about? it seems to pop out of thin air somehow.
also, I think I can grasp SO(7), but the derivation of G2 from the rotations seemed almost arbitrary: you created some vectors for convenience, noticed the rotation property failed when you added a specific element, then fixed it with a rotation element that fell into G2.
It feels like the integration of 1/cos(x) = ln(tan(x)+sec(x)) (metaphorically), as you would not know how to derive it unless you already knew the answer and worked backward.

[ValkyRiver]

Why don’t we just use Geometric Algebra and the wedge product?

[angeldude]

I thought a vector was just an object that can be added and scaled. (More formally, given vectors u and v, and a scalar a, then a(u + v) = (u + v)a = au + av; if that equality is satisfied, then u and v are vectors.)
What do you mean "the concept of an axis of rotation is doomed to fail in higher dimensions"? If by "axis" you mean "line", then yes, but who said you can't have an axis of rotation in 7-dimensions that's a 5-dimensional hyperplane? In general, axes of rotation are N-2 dimensional surfaces, though these are very distinct from "coordinate axes". Perhaps "axle" would be better than "axis" because of that.

[MrWorshipMe]

Why should we expect the cross product to transform to the cross product of the transformed vectors? There's another transformation vectors can make - scaling by a factor. In this case, the transformed cross product would not be the same as the cross product of the transformed vectors, even in 3 dimensions. It seems that it is a happy accident that the cross product is covariant in 3 dimensions, but it still isn't a vector...

[drdca]

I’m not sure I really follow the “it doesn’t transform like a vector” point?
Uhh,
well, if F(R(u), R(v)) ≠ R(F(u, v)) for rotation matrices R,
Well, that seems relevant, certainly,
but, for a particular u and a particular v, F(u, v) is still an element of a vector space...

I guess you’re just using “vector” to mean something subtly different, but I’m not sure exactly what it is?
Like,
well, I guess maybe I don’t get what you mean by “transforms like a vector”? As I think of vectors, when you change what basis you are using, the vector doesn’t change, only the representation of it in the basis you are using, changes.
I guess if you have a function which takes in representations of two vectors, in the same basis, and returns a representation of another vector in that basis,
but where what vector it produces changes based on the basis chosen,
then...
I guess then the function doesn’t really output a vector, so much as a description of a vector, so maybe that’s why you describe it as not being a vector?

I’ll keep watching the other 2/3 of the video now

[srghma]

similar to HoTT theory "we tried to understand what is equality, lift original notion of equality to higher types, but found that after 7th ( or I dont remember which level number, O_O) there are SEVERAL suitable definitions of equality

P.S. I didnt understand this video even little, but after humans will have Neuralink videos - I will be able to watch higher dimentional videos

(all slices of w-axis are shown to our brain as 2d images)


continue, it is important

[sahhaf]

As far as I know, cross product is only defined in 3D.