filmov
tv
The 3 Jugs Riddle

Показать описание
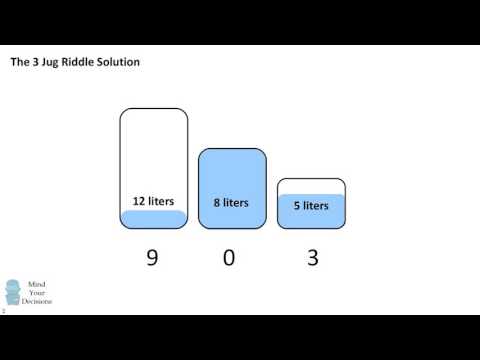
You have a full 12 liter jug and empty 5 and 8 liter jugs. Can you measure exactly 6 liters? This problem dates to 1484 and was posed in the context of a milkman making a home delivery to a customer. The story goes this riddle so delighted Simeon Denis Poisson as a young boy that it was one reason he pursued mathematics.
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
My Books
Connect on social media. I update each site when I have a new video or blog post, so you can follow me on whichever method is most convenient for you.
My Books
The 3 Jugs Riddle
The 3 Jug Riddle The Magic of Mathematics
Measure 4 Litres Bucket Problem || The 3 & 5 Litre Die Hard Water Puzzle || Interview Puzzles
Can You Solve The DIE HARD Water Jug Riddle?
The 3 Jug Riddle hd720
Puzzle #1: The 3 and 5 litre water jug problem
How to Measure 4 Litres, with a 5 Litre and 3 Litre Container - Step by Step Instructions - Tutorial
3 jugs | Math Riddle
How to Solve the Water Jug Riddle - (Classic Riddle Has Everyone Stumped)
8 Liter 5 liter 3 liter puzzle - Water quiz - 8 Litre - 5 litre - 3 litre - Water puzzle
Water Jug Riddle from Die Hard 3
Water Jug Riddle Measure 9L and 4L Water Puzzle | Riddles Answer
Die Hard 3 Water Riddle (Not Many Can Do This In Time)
The Water Jug Problem | Die Hard Water Riddle
Logical Reasoning Math Puzzle With Answer | Filling The Jugs
Water Jug Riddle | Measure 4L using 5L and 3L container | Fun Session
3 Jug Game /Puzzle
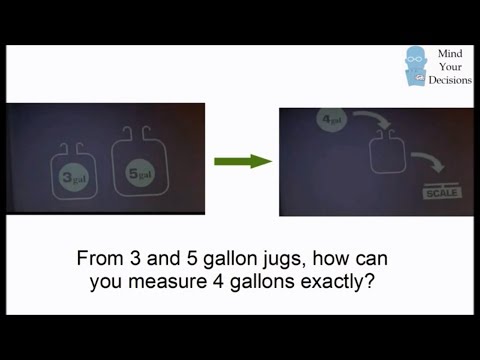
🔑 4 Gallons from 3-Gallon and 5-Gallon Jugs problem ! ! ! ! !
90% Cannot Solve This | Water Jug Riddle
IS 3 Jug Problem
Water Jug Riddle Measure 5L and 3L Water Puzzle | Riddles Answer
Level 6 of River Crossing Game | 8-liter 5-liter 3-liter puzzle | Water Jug Problem
Water Jug Puzzle Solution
The three switches puzzle: Solution
Комментарии
 0:03:10
0:03:10
 0:03:10
0:03:10
 0:03:09
0:03:09
 0:01:59
0:01:59
 0:03:10
0:03:10
 0:01:36
0:01:36
 0:02:09
0:02:09
 0:00:59
0:00:59
 0:03:59
0:03:59
 0:01:33
0:01:33
 0:01:53
0:01:53
 0:05:08
0:05:08
 0:02:06
0:02:06
 0:01:44
0:01:44
 0:01:53
0:01:53
 0:04:29
0:04:29
 0:11:39
0:11:39
 0:05:19
0:05:19
 0:00:55
0:00:55
 0:06:58
0:06:58
 0:03:43
0:03:43
 0:03:10
0:03:10
 0:00:47
0:00:47
 0:03:34
0:03:34