filmov
tv
Factoring polynomials into linear quadratic factors | Linear Algebra MATH1141 | N J Wildberger

Показать описание
Following on from the (necessarily approximate) Fundamental theorem of Algebra, we investigate real polynomials and their (necessarily approximate) factorization into linear and quadratic factors. To clarify this we look more carefully at cyclotomic factorizations of z^n-1 and the connections with roots of unity.
We also explain the computational hurdles in applying these theoretical results to actual real polynomials.
************************
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************************************
Here are the Insights into Mathematics Playlists:
****************
We also explain the computational hurdles in applying these theoretical results to actual real polynomials.
************************
Here are the Wild Egg Maths Playlists (some available only to Members!)
************************************************
Here are the Insights into Mathematics Playlists:
****************
Factoring polynomials into linear quadratic factors | Linear Algebra MATH1141 | N J Wildberger
How To Factor Polynomials The Easy Way!
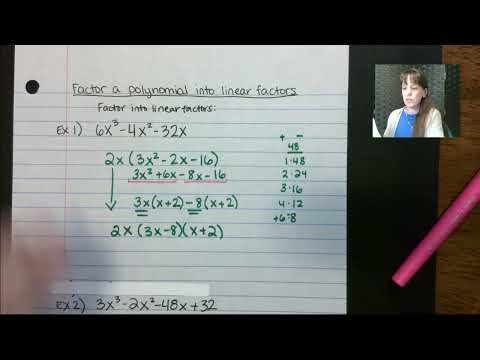
Factor a Polynomial Into Linear Factors
Write the Polynomial as a Product of Linear Factors and Find the Zeros
Example: Linear and Irreducible Quadratic Factors of a Polynomial (4)
Factoring polynomials using complex numbers | Khan Academy
FASTEST way to factor a trinomial! #shorts
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
Factoring 5-term polynomials by grouping
Factoring Trinomials
Find the Zeros of a Polynomial Then Write Out Using Linear Factorization
Factoring Quadratics... How? (NancyPi)
Factoring Trinomials & Polynomials, Basic Introduction - Algebra
Factoring a polynomial to the fourth power using factoring to second power
How to factor a hard 4th degree polynomial (no rational zero, can't do it by grouping)
Solving Polynomial Equations By Factoring and Using Synthetic Division
Quadratic Equations | Solve by factoring | Free Math Videos
Quickly learn how to factor a quadratic with three terms
Factoring Quadratic Expressions Pt. 1
Factorize The Polynomials P(Z) into Linear Factors
Example 6: Factoring quadratics with two variables | Algebra I | Khan Academy
Write the polynomial as a product of linear factors (Sect. 2.5, example #5)
Learn the ac method for factoring and solving a quadratic equation
GCSE Maths - Factorising Quadratics - Part 1 - (When the x^2 Coefficient is 1) - #50
Комментарии
 0:29:24
0:29:24
 0:11:54
0:11:54
 0:04:09
0:04:09
 0:04:17
0:04:17
 0:05:08
0:05:08
 0:03:10
0:03:10
 0:00:55
0:00:55
 0:12:29
0:12:29
 0:05:33
0:05:33
 0:04:17
0:04:17
 0:05:07
0:05:07
 0:09:14
0:09:14
 0:34:46
0:34:46
 0:03:26
0:03:26
 0:04:55
0:04:55
 0:14:19
0:14:19
 0:02:43
0:02:43
 0:01:16
0:01:16
 0:05:53
0:05:53
 0:14:17
0:14:17
 0:02:46
0:02:46
 0:04:17
0:04:17
 0:05:00
0:05:00
 0:06:24
0:06:24