filmov
tv
Triangle Inequality for Complex Numbers- 3 different proofs and other inequalities-Complex Variables
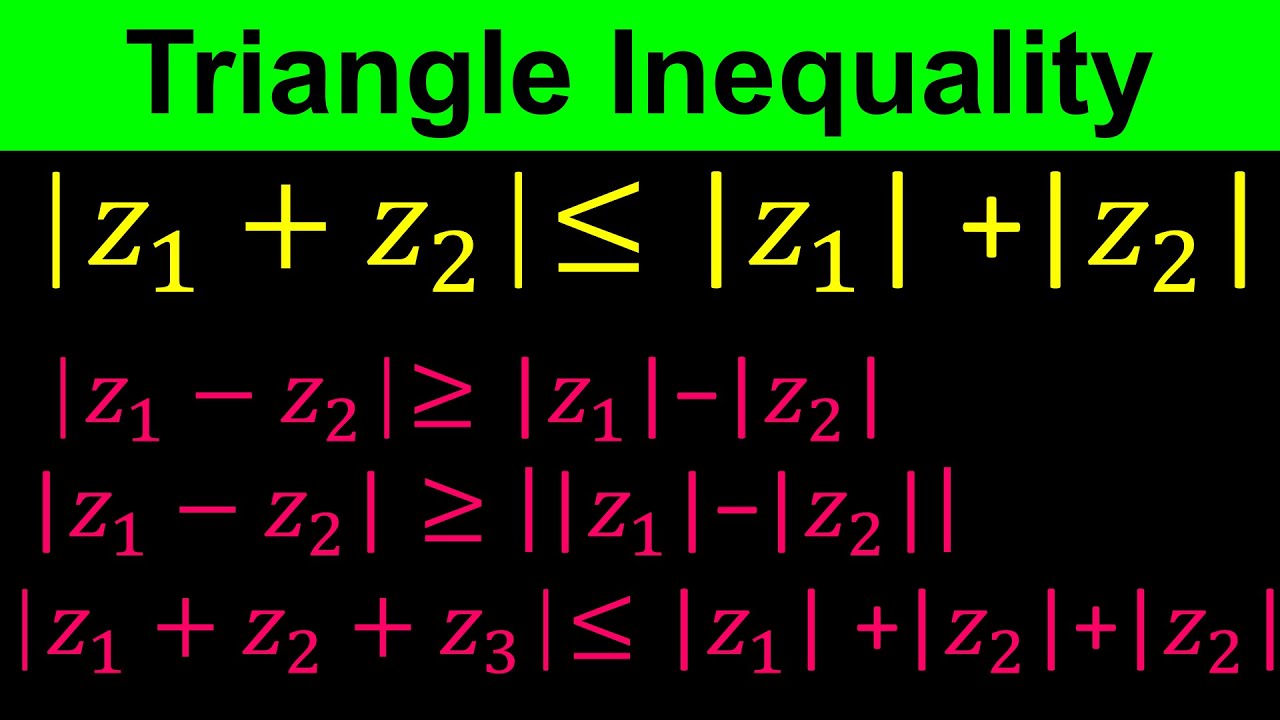
Показать описание
In this video we will learn about triangle inequality for complex numbers and also other inequalities for complex numbers. We prove the triangle inequality in three different methods.
Complex numbers are numbers that extend the concept of the one-dimensional number line to the two-dimensional complex plane. They consist of a real part and an imaginary part, and they are used in mathematics, physics, engineering, and other fields to solve problems that cannot be addressed using only real numbers.
Definition:
A complex number is written in the form:
z=a+bi,
where:
a: The real part of the complex number (Re(z)=a).
b: The imaginary part of the complex number (Im(z)=b).
i: The imaginary unit, defined as i=sqrt(-1)
, with the property that i^2=-1
Complex numbers are numbers that extend the concept of the one-dimensional number line to the two-dimensional complex plane. They consist of a real part and an imaginary part, and they are used in mathematics, physics, engineering, and other fields to solve problems that cannot be addressed using only real numbers.
Definition:
A complex number is written in the form:
z=a+bi,
where:
a: The real part of the complex number (Re(z)=a).
b: The imaginary part of the complex number (Im(z)=b).
i: The imaginary unit, defined as i=sqrt(-1)
, with the property that i^2=-1
 0:08:45
0:08:45
 0:09:24
0:09:24
 0:10:46
0:10:46
 0:07:00
0:07:00
 0:09:43
0:09:43
 0:05:52
0:05:52
 0:06:55
0:06:55
 0:12:18
0:12:18
 0:05:47
0:05:47
 0:08:49
0:08:49
 0:38:25
0:38:25
 0:00:05
0:00:05
 0:03:08
0:03:08
 0:04:59
0:04:59
 0:09:38
0:09:38
 0:05:46
0:05:46
 0:21:22
0:21:22
 1:32:44
1:32:44
 0:01:01
0:01:01
 0:12:43
0:12:43
 0:12:51
0:12:51
 0:04:49
0:04:49
 0:14:07
0:14:07
 0:11:59
0:11:59