filmov
tv
Olympiad Math Trick | Olympiad Challenging Question.

Показать описание
In this tutorial I will lead you on how to solve this kind/type of challenging Olympiad radical equation.
There are some substitutions in solving this mathematical challenge that really need your attention and focus in order for you to be able to grab them I strongly advise you stay glue to this video paying full attention and without skipping any parts of this video.
In solving this challenge, I will teach how to formulate simultaneous equation and even quadratic equation. I will guide you on how to solve all the formed equations step by step.
Do not forget to subscribe if you are new here.
Thanks!!!
#olympiad2022 #mathchallenge #onlinemathstv #onlinemaths #onlineclasses #online #mathstricks #olympiadmathematicscompetition #olympiadpreparation #simultaneousequations #elimination #eliminationmethod #quadraticformula #quadraticequation #mathsolution #solutions #mathsbasics #mathsbaba #solvingpuzzle #solving #solvingproblems #solvingequations #methods #realsolutions #steps #stepbystep #step #challengingmathproblems #maths #mathematics #math #calculation #calculating #moneytips #money #trickstosolvemcqs #moneytrick #puzzlemath #puzzle #puzzles
There are some substitutions in solving this mathematical challenge that really need your attention and focus in order for you to be able to grab them I strongly advise you stay glue to this video paying full attention and without skipping any parts of this video.
In solving this challenge, I will teach how to formulate simultaneous equation and even quadratic equation. I will guide you on how to solve all the formed equations step by step.
Do not forget to subscribe if you are new here.
Thanks!!!
#olympiad2022 #mathchallenge #onlinemathstv #onlinemaths #onlineclasses #online #mathstricks #olympiadmathematicscompetition #olympiadpreparation #simultaneousequations #elimination #eliminationmethod #quadraticformula #quadraticequation #mathsolution #solutions #mathsbasics #mathsbaba #solvingpuzzle #solving #solvingproblems #solvingequations #methods #realsolutions #steps #stepbystep #step #challengingmathproblems #maths #mathematics #math #calculation #calculating #moneytips #money #trickstosolvemcqs #moneytrick #puzzlemath #puzzle #puzzles
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
A beautiful international math olympiad problem
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Germany l can you solve?? l Hardest Olympiad Math problem
Luxembourg - Math Olympiad Question | You should know this trick
A Nice Math Olympiad Exponential Equation 3^x = X^9
New Zealand - Math olympiad Question
This U.S. Olympiad Coach Has a Unique Approach to Math
Japanese l can you solve this?? l Olympiad Math Problem
Norway Math Olympiad Question | You should be able to solve this!
Brazil l Very Nice Olympiad Exponential Problem l Easy & Tricky Solution
Germany - Math Olympiad Exponential Problem.
Math Olympiad Practice
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
Math Olympiad Challenge b³+b=30 |The Complete Solutions | Best Trick !!
Russia | Math Olympiad Question | You should know this trick!!
Mexico - A Nice Math Olympiad Exponential Problem
Japanese Math Olympiad Problem | A Nice Math Problem : Comparison
Maths Olympiad | A Tricky Maths Olympiad Questions | Algebra Problem |
The unexpectedly hard windmill question (2011 IMO, Q2)
A Very Nice Olympiad Math Exponential Problem l Easy & Tricky Solution
IMO Latest Pattern 2023-24 | Math Olympiad | BYJU’s #ytshorts #olympiad
1995 British Mathematics Olympiad problem
Germany - Math Olympiad Question | The BEST Trick
Комментарии
 0:00:52
0:00:52
 0:01:00
0:01:00
 0:01:54
0:01:54
 0:18:54
0:18:54
 0:02:51
0:02:51
 0:02:34
0:02:34
 0:01:12
0:01:12
 0:03:20
0:03:20
 0:16:46
0:16:46
 0:03:21
0:03:21
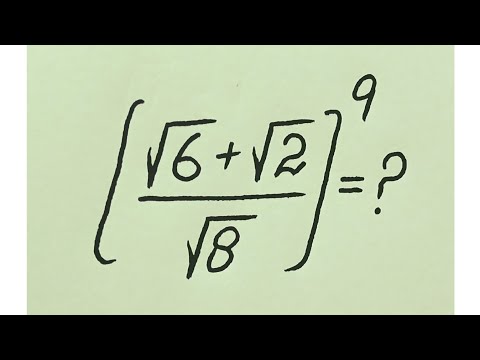 0:17:00
0:17:00
 0:04:45
0:04:45
 0:01:00
0:01:00
 0:07:26
0:07:26
 0:08:06
0:08:06
 0:08:01
0:08:01
 0:08:36
0:08:36
 0:04:15
0:04:15
 0:08:03
0:08:03
 0:16:03
0:16:03
 0:09:17
0:09:17
 0:00:39
0:00:39
 0:20:59
0:20:59
 0:10:37
0:10:37