filmov
tv
The Sum of Discrete and Continuous Random Variables

Показать описание
MIT 6.041SC Probabilistic Systems Analysis and Applied Probability, Fall 2013
Instructor: Jagdish Ramakrishnan
License: Creative Commons BY-NC-SA
Instructor: Jagdish Ramakrishnan
License: Creative Commons BY-NC-SA
The Sum of Discrete and Continuous Random Variables
L12.2 The Sum of Independent Discrete Random Variables
RULE of SUM and RULE of PRODUCT - DISCRETE MATHEMATICS
[Discrete Mathematics] Rule of Sum and Rule of Product Examples
Discrete and continuous random variables | Probability and Statistics | Khan Academy
[Discrete Mathematics] Rule of Sum and Rule of Product
Discrete Math II - 6.1.1 The Rules of Sum and Product
Summation Formulas and Sigma Notation - Calculus
Solve with us -week 7
Discrete Math - 2.4.3 Summations and Sigma Notation
Discrete random variable problem/ application of discrete random variable
02 - Random Variables and Discrete Probability Distributions
Counting principles - rule of product & sum || Discrete Structures
Period of a sum of two discrete complex exponentials
Sum and Product Principles for Finite Sets [Discrete Math Class; Visual Proof]
what is sigma notation and how to we use it
Expected Value and Variance of Discrete Random Variables
Sum of Two Independent Identically Distributed Discrete RVs (Introduction to Discrete Convolution)
DISCRETE PROBABILITY DISTRIBUTION: FINDING THE UNKNOWN PROBABILITIES.
Discrete Math 2.4.3 Intro to Summations
GATE 2024 | Discrete Mathematics | Summation | Computer Science Engineering | BYJU'S GATE
RANDOM VARIABLES I DISCRETE AND CONTINUOUS I GRADE 11 STATISTICS AND PROBABILITY I EPISODE 1
Discrete Time Convolution Example
Basics of Computing || Sum rule || Product Rule || Combinatorics || Discrete Mathematics || DMS
Комментарии
 0:05:37
0:05:37
 0:07:52
0:07:52
 0:09:23
0:09:23
![[Discrete Mathematics] Rule](https://i.ytimg.com/vi/t0us-MXrFZg/hqdefault.jpg) 0:06:00
0:06:00
 0:11:56
0:11:56
![[Discrete Mathematics] Rule](https://i.ytimg.com/vi/MmzJF2L_5PA/hqdefault.jpg) 0:11:12
0:11:12
 0:19:37
0:19:37
 0:20:24
0:20:24
 2:01:09
2:01:09
 0:06:40
0:06:40
 0:10:22
0:10:22
 0:29:54
0:29:54
 0:10:52
0:10:52
 0:06:58
0:06:58
 0:02:35
0:02:35
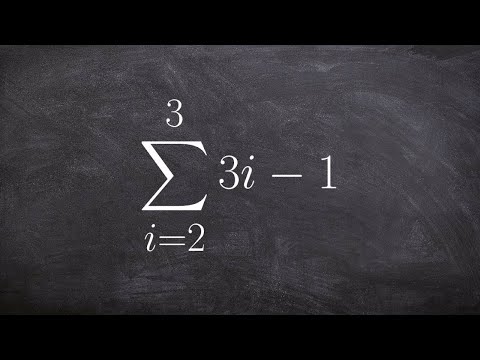 0:01:22
0:01:22
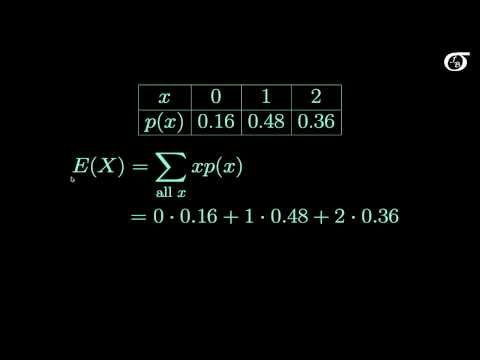 0:07:57
0:07:57
 0:19:05
0:19:05
 0:05:29
0:05:29
 0:06:11
0:06:11
 0:47:20
0:47:20
 0:12:47
0:12:47
 0:10:10
0:10:10
 0:11:11
0:11:11