filmov
tv
derivatives 'defined' without limits?!?
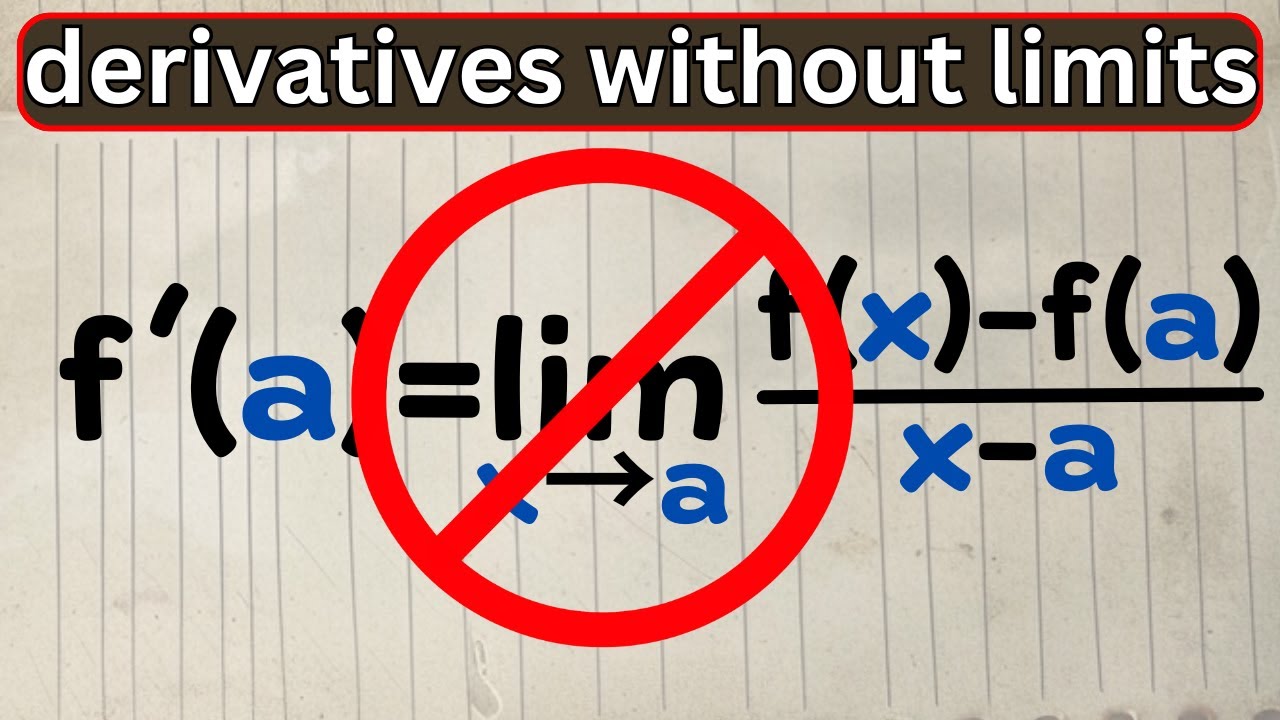
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
derivatives 'defined' without limits?!?
Visual Derivative Definition!
The definition of a derivative
HOW TO SET UP THE LIMIT DEFINITION OF THE DERIVATIVE | Calculus Derivatives
Definition of the Derivative
Finding Derivatives using Infinitesimals (no limits)
Calculus WITHOUT limits!
Proof of basic derivatives WITHOUT limits!
Final Exam Review : Calculus 2 Part 8
Limits and Derivatives
Calculus Basics: What is a Derivative?
Limits, L'Hôpital's rule, and epsilon delta definitions | Chapter 7, Essence of calculus
Limit Definition of the Derivative of a Function
The paradox of the derivative | Chapter 2, Essence of calculus
Derivation of e^x without limits or calculus.
Finding the Derivative of a Polynomial Function | Intro to Calculus #shorts #math #maths
Understand Calculus in 35 Minutes
Where Does the Definition of the Derivative Come From?
Calculus 1 - Introduction to Limits
Derivatives... What? (NancyPi)
'tricky' derivatives with the limit definition.
Visualizing the derivative of sin(x)
Mainstream calculus without flawed limit theory
Using the Limit Definition of Derivative
Комментарии
 0:15:50
0:15:50
 0:01:00
0:01:00
 0:01:00
0:01:00
 0:06:12
0:06:12
 0:23:31
0:23:31
 0:13:32
0:13:32
 0:17:29
0:17:29
 0:14:27
0:14:27
 11:28:27
11:28:27
 0:05:23
0:05:23
 0:00:56
0:00:56
 0:18:27
0:18:27
 0:12:39
0:12:39
 0:16:50
0:16:50
 0:03:20
0:03:20
 0:01:01
0:01:01
 0:36:22
0:36:22
 0:04:26
0:04:26
 0:20:20
0:20:20
 0:14:30
0:14:30
 0:11:58
0:11:58
 0:00:59
0:00:59
 0:12:31
0:12:31
 0:07:03
0:07:03