filmov
tv
Finding the Derivative of a Polynomial Function | Intro to Calculus #shorts #math #maths
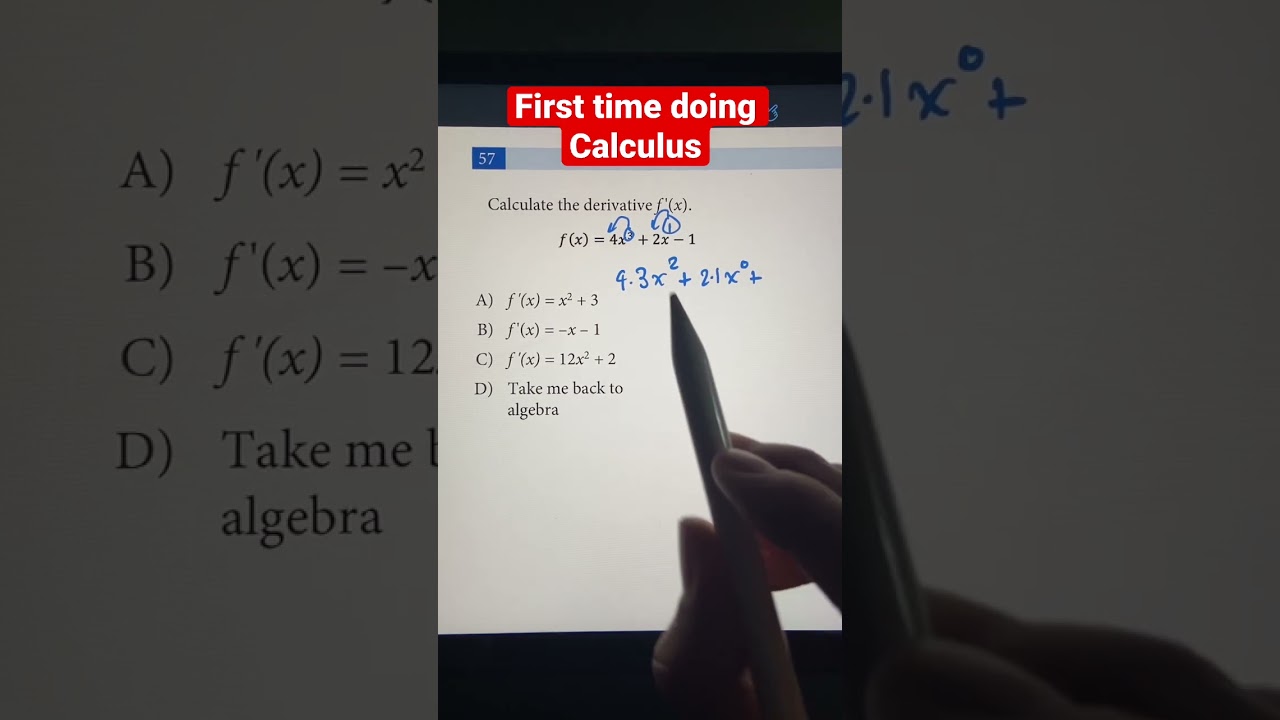
Показать описание
Definition of the Derivative
Calculus - How to find the derivative of a function using the power rule
Basic Derivative Rules - The Shortcut Using the Power Rule
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
Derivative from First Principles
What is a derivative?
Derivative by first principle- Example 2.
Chain Rule For Finding Derivatives
AS Level Maths | Differentiation From First Principles | Learn With Ryan
How To Find The Derivative of a Fraction - Calculus
Calculus - Finding the derivative of a function using limits
Finding the Derivative of a Polynomial Function | Intro to Calculus #shorts #math #maths
Find the derivative using the power rule
How to find the derivative of a function using the sum and difference rule
Understand Calculus in 35 Minutes
Differential Calculus: Finding the derivative of a quadratic equation
BASIC DERIVATIVE OF ALGEBRAIC FUNCTIONS || BASIC CALCULUS
Finding first and second derivative
Find the derivative
First Derivative grade 12: Practice
Take the derivative of the natural log function
Learn how to find the derivative of the integral
Taking the derivative of two binomials using product and chain rule
Finding the Derivative from First Principles - AS Level/Year 12 Mathematics
Комментарии
 0:23:31
0:23:31
 0:05:21
0:05:21
 0:05:34
0:05:34
 0:07:16
0:07:16
 0:07:35
0:07:35
 0:10:43
0:10:43
 0:04:54
0:04:54
 0:18:40
0:18:40
 0:13:58
0:13:58
 0:14:38
0:14:38
 0:04:36
0:04:36
 0:01:01
0:01:01
 0:01:21
0:01:21
 0:02:47
0:02:47
 0:36:22
0:36:22
 0:00:51
0:00:51
 0:20:11
0:20:11
 0:07:03
0:07:03
 0:09:04
0:09:04
 0:01:05
0:01:05
 0:00:43
0:00:43
 0:01:25
0:01:25
 0:04:44
0:04:44
 0:20:14
0:20:14