filmov
tv
Olympiad Geometry Problem #6: Isosceles Triangle, Parallels, Perpendicular
Показать описание
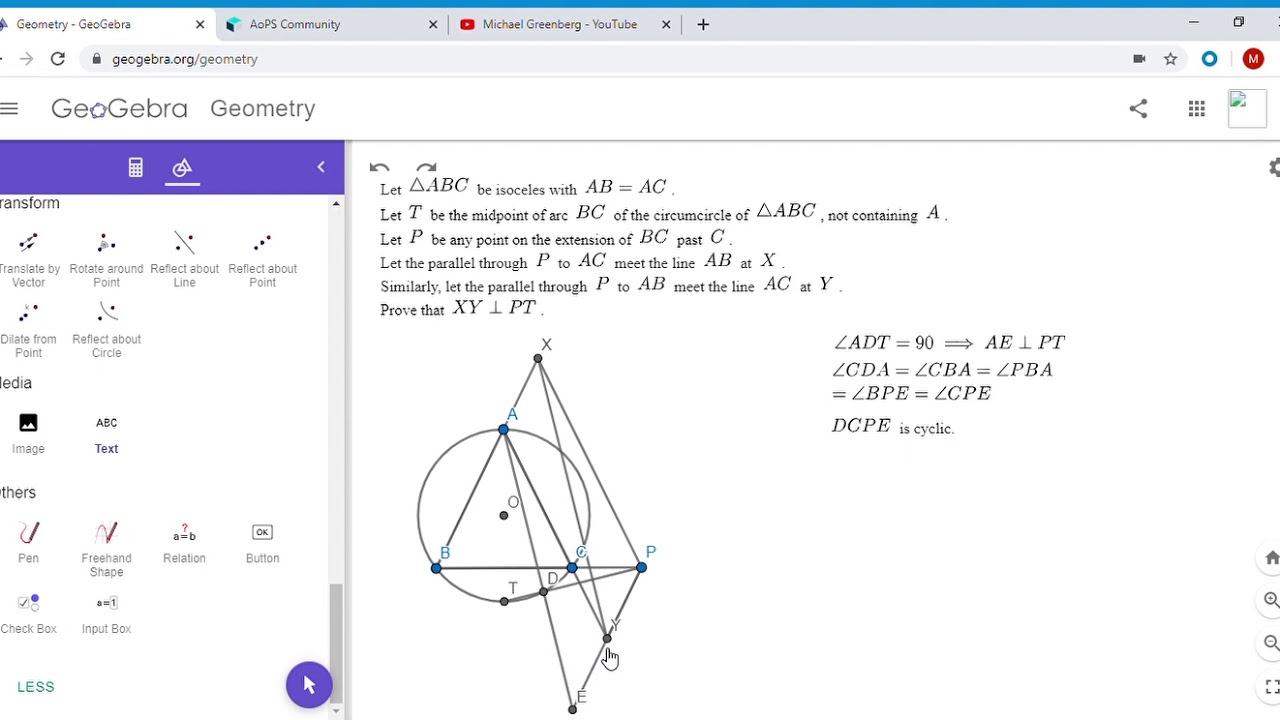
Here is a very fun problem from the 2005 Iran Team Selection Test, used to select the team for the International Math Olympiad. Enjoy! Link below.
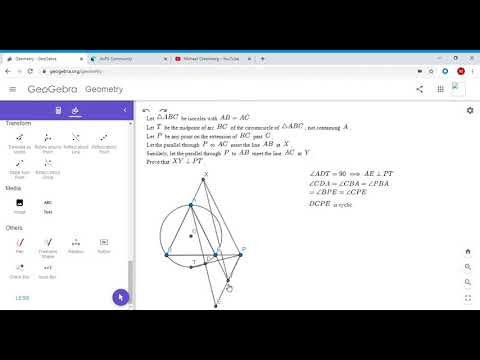
Olympiad Geometry Problem #6: Isosceles Triangle, Parallels, Perpendicular
Olympiad Geometry Problem #7: Isosceles Triangle, Midpoint, Equal Angles
Find the angle BXC in the isosceles triangle. Geometry Challenge. Math Olympiad Geometry problem.
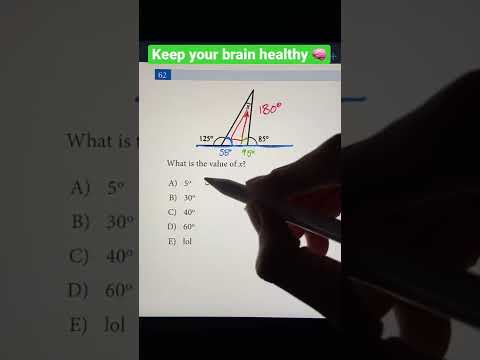
Don’t make this “Silly Mistake” from “Triangles” 🤯 | PYQ | #ytshorts #boards2024 #class10...
Olympiad Geometry Problem #32: IMO 2019 #6
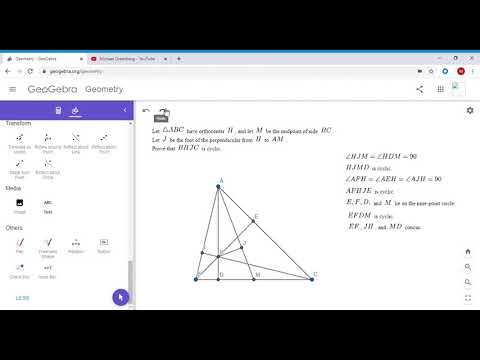
Olympiad Geometry Problem #10: Isosceles Triangle, Midpoints, Perpendiculars
Olympiad Geometry Problem #5: H-M Theorem
Olympiad Geometry Problem #42: Isosceles Triangle, Median, Altitude, Midpoint
Q481 | Math Olympiad | Geometry | Isosceles Right Triangle | Angle Bisector Theorem
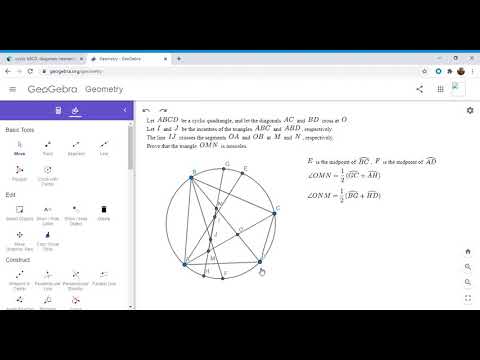
Olympiad Geometry Problem #36: Cyclic Quad, Incenters, Isosceles
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
Why are all teachers scared of this date? - 17th July | #shorts
TRICKS you can do in SCIENTIFIC CALCULATORS🔥#viral #shorts
Olympiad Geometry Problem #73: IMO Shortlist 2005 G6
Topper Vs Back bencher | Exterior Angle Property #shorts #youtubeshorts #ashortaday #viralmaths #fun
Can You Find Angle X? | Geometry Challenge!
Olympiad Geometry Problem #93: Two Isosceles Triangles, Circumcircle, Perpendicular
Math Olympiad Problems | A Nice olympiad geometry Problem | Explain with easy way
Cotan 30° + Cotan 75° = ? ABC - an isosceles triangle. Math Olympiad Geometry and Algebra problem.
Olympiad Mathematics | Find area of the pink square | (Isosceles triangles) | #math #maths
Area and perimeter of square | Ayushi teacher | Area and perimeter #maths #area #perimeter
Sneha Pareek(topper)checking Jee mains result 2022//score 300/300
A Nice Math Olympiad Geometry Problem | 2 Methods to Solve
2022 China Math Olympiad: Calculate A Square Pyramid Volume (fill-in-the-blank problem)
Комментарии
 0:10:55
0:10:55
 0:10:08
0:10:08
 0:04:10
0:04:10
 0:00:41
0:00:41
 0:20:24
0:20:24
 0:11:05
0:11:05
 0:12:01
0:12:01
 0:13:46
0:13:46
 0:03:02
0:03:02
 0:11:57
0:11:57
 0:00:44
0:00:44
 0:00:48
0:00:48
 0:00:25
0:00:25
 0:13:34
0:13:34
 0:00:13
0:00:13
 0:08:44
0:08:44
 0:12:26
0:12:26
 0:10:51
0:10:51
 0:03:26
0:03:26
 0:10:46
0:10:46
 0:00:16
0:00:16
 0:00:35
0:00:35
 0:19:58
0:19:58
 0:00:58
0:00:58