filmov
tv
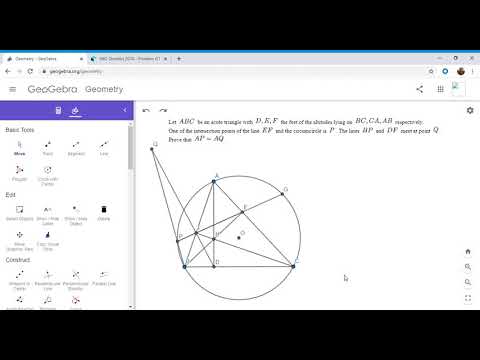
Olympiad Geometry Problem #18: Altitudes, Circumcircle, Equal Segments

Показать описание
This is the first problem I have done from an IMO Shortlist. It was the easiest geometry problem on the 2010 IMO Shortlist, and I hope to do more such problems. See the link below, hope you all enjoy!
Olympiad Geometry Problem #18: Altitudes, Circumcircle, Equal Segments
olympiad geometry problem #geometry
Olympiad Geometry Problem #83: Tangency, Circumcircle, Bisection
Olympiad Geometry Problem #22: Perpendiculars, Parallel, Cyclic
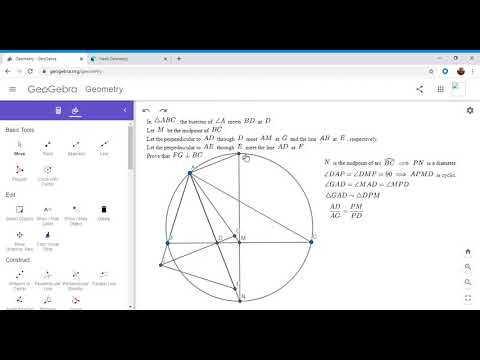
Olympiad Geometry Problem #17: Blanchett's Theorem
Olympiad Geometry Problem #16: 60 Degrees, Bisector, Reflection
MATH OLYMPIAD | GEOMETRY | TRIANGLES | MEDIANS AND ALTITUDE RELATED QUESTION | YOU MUST LEARN |
A Good Math Olympiad Geometry Problem | Math Olympiad Questions |#maths #math #geometry #algebra
Missing Angles Geometry Problem | Tricky Math Question | JusticeTheTutor #maths #math #shorts
NEWYES Calculator VS Casio calculator
Olympiad Geometry Problem #52: Symmedian Theorem
India vs japan || mathematics challenge || 😅🤣🤣🤭
Olympiad Geometry Problem #19: Angle Bisector, Perpendiculars, Midpoint
Math Olympiad #1: Triangle Altitude.
A case that shocked Canada in 2012😳 #shorts
Denmark 2022 Math Olympiad Problem | Math Olympiad Problems | Explain important Geometry skill
Olympiad Geometry Theorems | L to P
IMONST 2020 Problems |Senior #18-20
Canadian Mathematical Olympiad 2017, problem 4 (geometry)
Olympiad Geometry Problem #56: 30 Degree Angle, Find Length
Geometry problems | Part 18 (Problems by Ahmad Demir)
WHY I HATE MATH 😭 #Shorts
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Olympiad Geometry Problem #13: Diameter, Tangent, Equal Segments
Комментарии
 0:12:18
0:12:18
 0:06:06
0:06:06
 0:12:32
0:12:32
 0:12:37
0:12:37
 0:11:39
0:11:39
 0:11:08
0:11:08
 0:05:28
0:05:28
 0:08:02
0:08:02
 0:00:37
0:00:37
 0:00:14
0:00:14
 0:07:45
0:07:45
 0:00:12
0:00:12
 0:11:30
0:11:30
 0:07:22
0:07:22
 0:00:14
0:00:14
 0:09:01
0:09:01
 0:07:39
0:07:39
 0:15:19
0:15:19
 0:27:25
0:27:25
 0:05:57
0:05:57
 0:09:13
0:09:13
 0:00:24
0:00:24
 0:00:12
0:00:12
 0:09:00
0:09:00