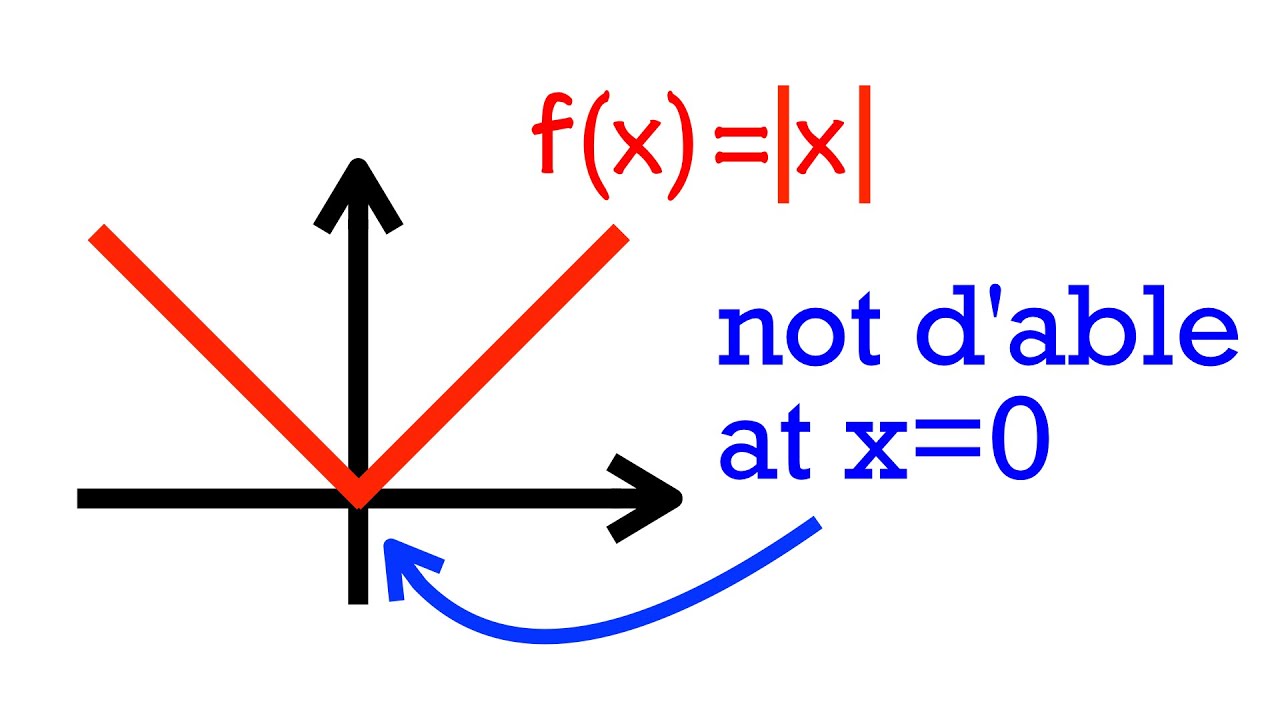
Why isn't abs(x) differentiable at x=0? (definition of derivative)

We will use the definition of derivative to show f(x)=abs(x) is not different x=0.
This is a classic counterexample that continuous functions might not be .

For more calculus tutorials, please see my new "just calculus" channel:

If you find my videos helpful, then consider supporting me on Patreon:

[notspaso]

I lost it when you said "this is not 'lol', this is |0|" comedy + maths, you're the best C:

[somebodysomewhere]

*This is not lol*
best quote from mathematics

[OonHan]

Homework: Why isn't abs(x) differentiable at x=0?
Me: "sites this video"

[leydigomezbravo]

Hi. I have been following you for 2 months and I like your videos. I really like the effort you give them and how they get to transmit. Thank you.

[DonSolaris]

*OMG!* the guy's talking to the ball!!! And i thought i saw everything on the Youtube.

[duckymomo]

It has two slopes, it’s a contradiction

[speedspeed]

I have a good handle of my calc classes. When we have study groups, I usually teach everyone on the board the way you and Peyman present stuff. You guys inspire me to make it fun, and competitive.

[banderfargoyl]

A function is discontinuous when the left limit doesn't equal the right limit. So you could say that a continuous function is non-differentiable when the left derivative doesn't equal the right one.

[yahelck]

You can also find the derivative of sqrt(x^2) and get x/sqrt(x^2).
At x=0 the derivative is equal to 0/0 which is undefined.

[VaradMahashabde]

We could use the epsilon-omega definition of a derivative and show that (|0|)' = 0.
In general then, (|x|)' = { 1 if x > 0, -1 of x < 0, 0 of x = 0}

[mwtxelo]

absolutely hated calculus at college but really enjoyed this video. thank you <3

[qtmeet]

I understand what you explained and that in this case the slope at 0 is undetermined because you can consider it having two slopes at that point, and a function can only have one y output, but I was thinking that-
Maybe you could write |x| as x*sgn(x) and then the derivative is just sgn(x), and sgn(0)=0

[weerman]

#subbed before you hit 25k :D Your channel has grown so fast the past year! yay

[evreng]

Also, we can write abs(x) as 2 functions. For x<=0, y=-x and for x>0, y=x. Then we can look their derivatives and as they are not same, their joint point has no derivative.

[secretsquirrel]

Why didn’t I know about you when I was struggling through calc 2 last semester! 😭

[alanhiguera]

another way to show that abs(x) is not differentiable at 0 is to define abs(x)=sqrt(x^2). differentiating abs with this defintion gives the derivative function as x/abs(x) which is not defined at x=0.

[sabriath]

One side should be clamped in order to make the integration continuous, otherwise you end up with a disjoint when going is not disjointed. In this case, you can actually have both sides use "0" simultaneously, you just have to note which direction:

y = {-1 if x<=0-, 1 if x>=0+

Because if you don't, when someone were to say "what's the integration from 0 to 5" of that function, "0" cannot be evaluated, yet |x| does contain the valid positive area. If someone said to find the area from -5 to 5, you would have to break it up as -5 to 0- and 0+ to 5.

etc. etc.

[craig]

Thank you! I was looking everywhere on how understand and do this!

[WolfgangBrehm]

The sign function looks like the derivative of |x| but it is defined at 0 to be 0. When we integrate sign(x) dx we get x sign(x), which is identical to |x|. So why is the derivative of x sign(x) not equal to sign(x) ?

[jaypeethegoat]

This example was a very difficult exercise at Panhellenics Exams in Greece in 2017 for the first time in the world!