filmov
tv
Solving (x - 2y - 3)dx + (2x + y - 1)dy = 0

Показать описание
00:00 Intro
01:00 Introducing X, Y, h, & k
04:02 The Simplified Problem
05:20 Getting dY/dX
06:07 Introducing v(x) and Simplifying
11:07 Integrating
13:56 Final Answer (Almost)
14:13 Forgetting to multiply tan by 2
14:14 Final Answer (Almost)
16:08 Remembering the missing 2
16:23 Final Simplified Answer
17:25 Outro
If you would like to see more content like this or you have any recommendations please leave a comment down below with what you'd like to see! Thanks for watching!
Note
If any mistakes are made please let me know in the comments down below, I'm only human and will endeavour to be correct as much as I can!
01:00 Introducing X, Y, h, & k
04:02 The Simplified Problem
05:20 Getting dY/dX
06:07 Introducing v(x) and Simplifying
11:07 Integrating
13:56 Final Answer (Almost)
14:13 Forgetting to multiply tan by 2
14:14 Final Answer (Almost)
16:08 Remembering the missing 2
16:23 Final Simplified Answer
17:25 Outro
If you would like to see more content like this or you have any recommendations please leave a comment down below with what you'd like to see! Thanks for watching!
Note
If any mistakes are made please let me know in the comments down below, I'm only human and will endeavour to be correct as much as I can!
Solving System of Linear Equations by SUBSTITUTION: 𝑥 – 2𝑦 = 1 and 2𝑥 – 4𝑦 = 2 | Algebra Solution...
Solving an equation for y and x using two steps
Solving an equation for y and x
How to Graph the Linear Equation x + 2y = 2
Given x+2y=5 Find 2 solutions of the equation, graph the 2 points, find the slope
Solving the differential equation xy'+2y=x^3
Find the slope: x+2y=-8
How to Graph the Linear Equation 2y = x
How to solve a pair of linear equations in 2 variables Class 10 Live Stream #Tutorix
Solve the differential equation (x-y)dy/dx=x+2y
solve the following 2x-y=4 x+2y=7
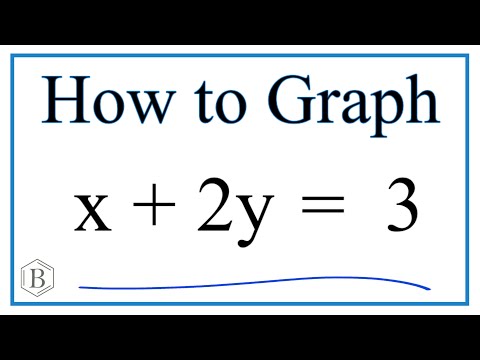
How to Graph the Linear Equation x - 2y = 3
Solve by matrix method x+2y=2 & 2x+3y=3 good example(PART-1)
How to Graph the Linear Equation x + 2y = 8
How to Graph the Linear Equation x + 2y = 4
How to Graph the Linear Equation x + 2y = 3
Check which of the following are solutions of the equation x-2y=4 and which are not
How to Graph the Linear Equation x + 2y = 6
solve the following equations graphicallly. 2x+3y=2 x-2y=8
Elimination: Solve the system x+2y=3, x-3y=-2
If 2x + y = 7 and x + 2y = 5, then PS02338
2x - 3y = 2; x + 2y = 8. Solve using Substitution Method.
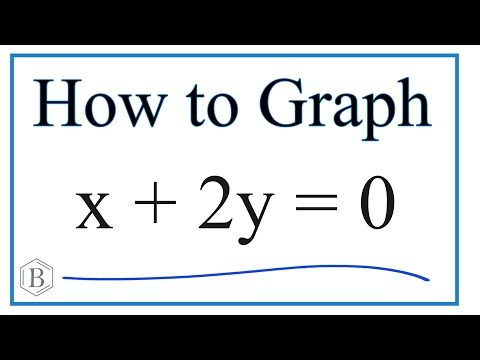
How to Graph the Equation x + 2y = 0
How to Graph the Linear Equation x + 2y = 6
Комментарии
 0:01:01
0:01:01
 0:03:12
0:03:12
 0:03:47
0:03:47
 0:01:53
0:01:53
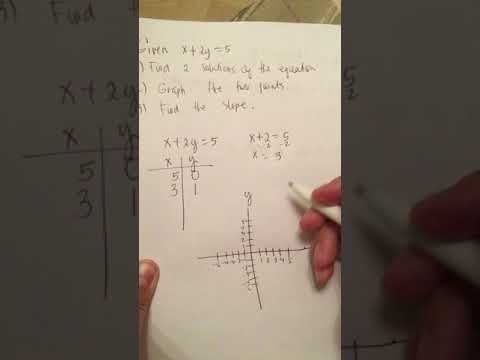 0:03:17
0:03:17
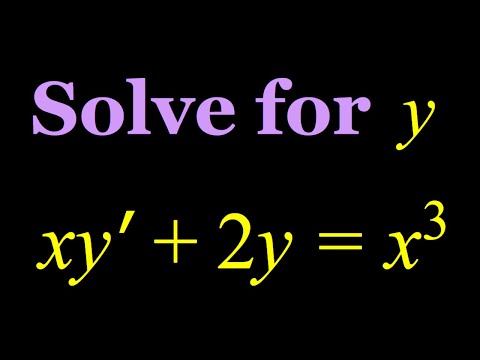 0:08:16
0:08:16
 0:02:26
0:02:26
 0:01:37
0:01:37
 0:58:05
0:58:05
 0:13:55
0:13:55
 0:02:00
0:02:00
 0:02:03
0:02:03
 0:05:12
0:05:12
 0:02:15
0:02:15
 0:02:15
0:02:15
 0:02:00
0:02:00
 0:04:10
0:04:10
 0:02:00
0:02:00
 0:03:45
0:03:45
 0:00:35
0:00:35
 0:01:09
0:01:09
 0:03:38
0:03:38
 0:01:45
0:01:45
 0:02:19
0:02:19