filmov
tv
Derivative of a linear combination (replaces the sum, difference and constant multiple rules).
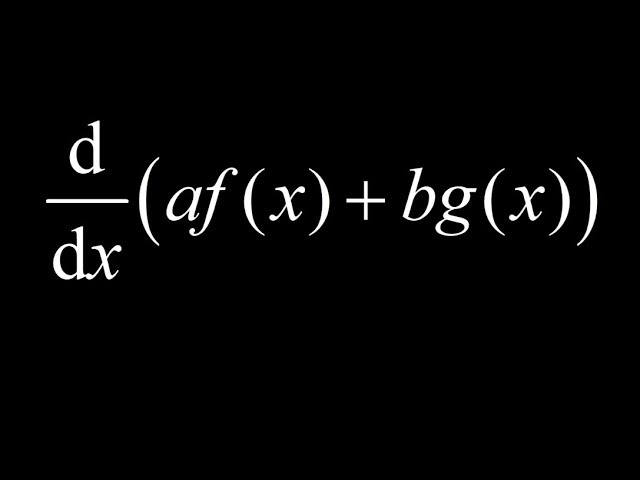
Показать описание
af(x)+bg(x) is called a linear combination of the functions f(x) and g(x). If we can derive a general rule for the derivative of a linear combination, then this rule replaces the sum, difference and constant multiple rules because those are all special cases of the linear combination rule! So why not use one rule instead of three?
To find the derivative of the linear combination, we apply the limit definition of the derivative limit as h approaches zero of L(x+h)-L(x) over h, where L is af(x) + bg(x). We evaluate the linear combination at x+h and x, take the difference and collect the f and g terms together. Breaking the whole thing into two limits and factoring out constants, we find the derivatives of the individual functions and arrive at a derivative rule for linear combinations: d/dx(af(x)+bg(x))=af'(x)+bg'(x).
In the previous video we learned how to differentiate power functions (functions of the form x^n), and now we know how to differentiate linear combinations of functions. This means we can now take the derivative of a polynomial!
We finish with two examples of derivatives of polynomials, one using Liebniz notation and one using prime notation. We take the derivative of 2x^2+3x-5 and the derivative of 5-4x^3+x^5.
To find the derivative of the linear combination, we apply the limit definition of the derivative limit as h approaches zero of L(x+h)-L(x) over h, where L is af(x) + bg(x). We evaluate the linear combination at x+h and x, take the difference and collect the f and g terms together. Breaking the whole thing into two limits and factoring out constants, we find the derivatives of the individual functions and arrive at a derivative rule for linear combinations: d/dx(af(x)+bg(x))=af'(x)+bg'(x).
In the previous video we learned how to differentiate power functions (functions of the form x^n), and now we know how to differentiate linear combinations of functions. This means we can now take the derivative of a polynomial!
We finish with two examples of derivatives of polynomials, one using Liebniz notation and one using prime notation. We take the derivative of 2x^2+3x-5 and the derivative of 5-4x^3+x^5.
 0:01:56
0:01:56
 0:04:37
0:04:37
 0:08:38
0:08:38
 0:08:01
0:08:01
 0:02:34
0:02:34
 0:03:46
0:03:46
 0:09:59
0:09:59
 0:04:26
0:04:26
 0:01:40
0:01:40
 0:05:39
0:05:39
 0:22:02
0:22:02
 0:09:44
0:09:44
 0:13:51
0:13:51
 0:16:37
0:16:37
 0:05:18
0:05:18
 0:10:55
0:10:55
 0:13:33
0:13:33
 0:13:21
0:13:21
 0:14:31
0:14:31
 0:12:03
0:12:03
 0:16:21
0:16:21
 0:01:00
0:01:00
 0:00:12
0:00:12
 0:45:52
0:45:52