filmov
tv
Doing calculus with a matrix!

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟Suggest a problem🌟
Doing calculus with a matrix!
How to Make it Through Calculus (Neil deGrasse Tyson)
Gilbert Strang: Linear Algebra vs Calculus
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Intro to Matrices
Linear transformations and matrices | Chapter 3, Essence of linear algebra
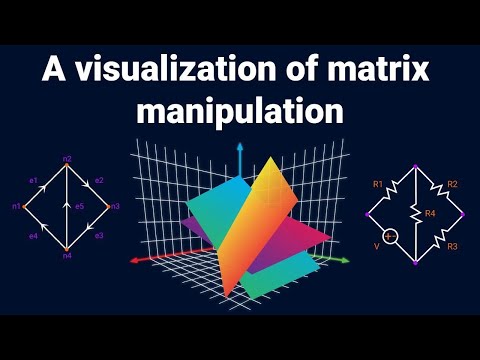
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
The Gaussian and Mean Curvatures of a Surface
ALL of calculus 3 in 8 minutes.
Essence of linear algebra preview
Introductory Calculus: Oxford Mathematics 1st Year Student Lecture
Integration (Calculus)
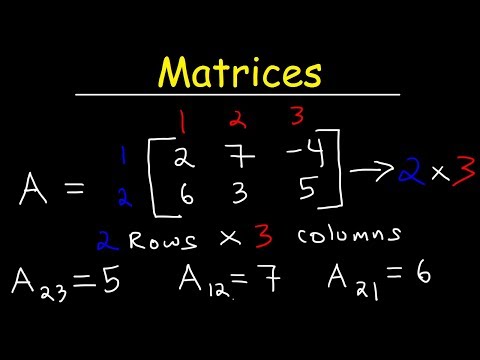
Understanding Matrices and Matrix Notation
Gaussian Elimination & Row Echelon Form
This is why you're learning differential equations
Baby calculus vs adult calculus
What is a determinant?
How (and why) to raise e to the power of a matrix | DE6
Gauss Jordan Elimination & Reduced Row Echelon Form
CSEC and CAPE ultimate! calculator tips | matrices quadratics simultaneous eqns calculus
The Hessian matrix | Multivariable calculus | Khan Academy
231 - [ENG] Introduction To Matrix Calculus
Vectors | Chapter 1, Essence of linear algebra
Pre-Calculus - Solve a system of equations using a matrix
Комментарии
 0:13:21
0:13:21
 0:03:38
0:03:38
 0:02:14
0:02:14
 0:00:09
0:00:09
 0:11:23
0:11:23
 0:10:59
0:10:59
 0:16:26
0:16:26
 0:10:26
0:10:26
 0:08:10
0:08:10
 0:05:09
0:05:09
 0:58:03
0:58:03
 0:07:04
0:07:04
 0:05:26
0:05:26
 0:18:40
0:18:40
 0:18:36
0:18:36
 0:00:27
0:00:27
 0:02:51
0:02:51
 0:27:07
0:27:07
 0:10:51
0:10:51
 0:42:58
0:42:58
 0:06:10
0:06:10
![231 - [ENG]](https://i.ytimg.com/vi/Eb9c-ACvOjo/hqdefault.jpg) 0:04:43
0:04:43
 0:09:52
0:09:52
 0:20:02
0:20:02