filmov
tv
Square, Semicircle, Quarter circle
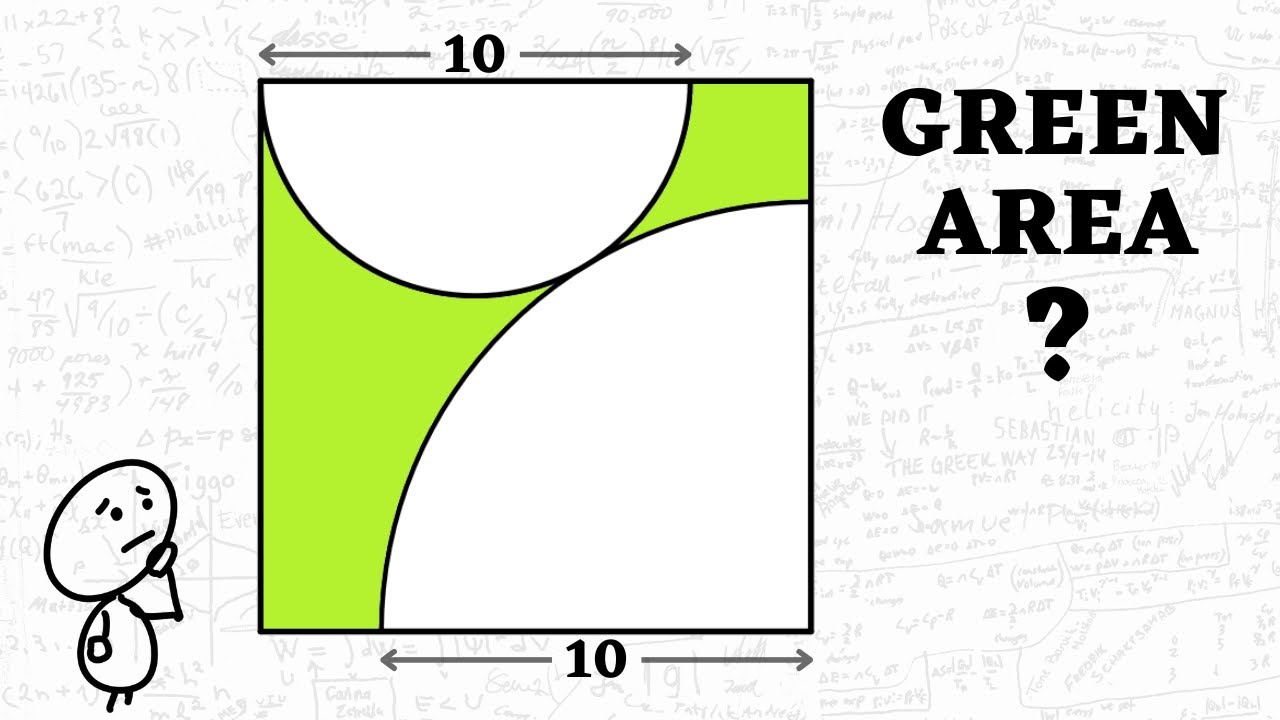
Показать описание
Square, Semicircle, Quarter circle
Square, Semicircle and Quarter circle: What is the yellow area?
Area of Square | Semicircle and Quarter Circle inside square problem | Advanced math problems
Geometry : Area of the Shadow Shape | Quarter Circle and Semicircle in a Square | Math Accelerator
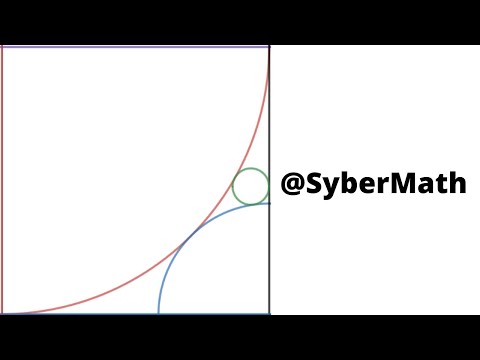
Two Semicircles and a Square in a Quarter Circle
WORLD CUP Problem -Quarter Circle inside a Square - Challenging Geometry
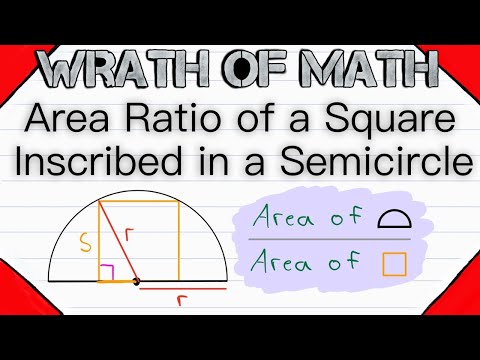
Area Ratio of Square Inscribed in a Semicircle | Geometry
A hard Area of Circle Puzzle Lying Inside the Square and Outside a Quarter Circle and a Semicircle
Mathematics Grade 9 November 2023 Paper 2 Memo Term 4 Exam @mathszoneafricanmotives
Semi Circle And Quarter Circle I Grade 2 I SNC I Mathematics I PEN Academy
Finding the Perimeter of a Combined Semicircle and Square!
Area of Semicircle | Semicircle inside Quarter Circle problem | Advanced math problems | Mathematics
Find the blue shaded area | Given a semicircle inside a quarter circle | Geometry Problem | 2 Method
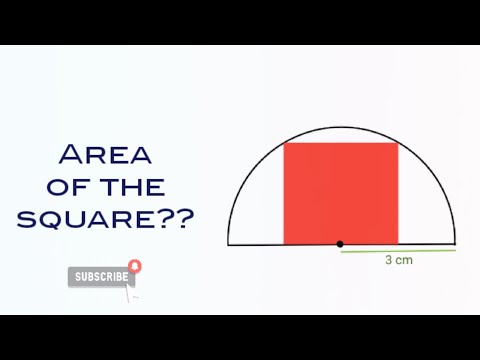
Area of the largest square inscribed in a semicircle| geometry| @logicxonomy
Area of Circle | Circle inside Quarter Circle and Square problem | Advanced math problems | Geometry
Area of a Quarter Circle - Corbettmaths
Area of Circle | Circle inside Quarter Circle and Square problem | Advanced math problems | Geometry
A circle, a semicircle, and a quarter circle
Two Semicircles and a Square in a Quarter Circle
Area : How to find the area of a semi-circle
Can you find area of the Yellow shaded Quarter circle? | (Square) | #math #maths | #geometry
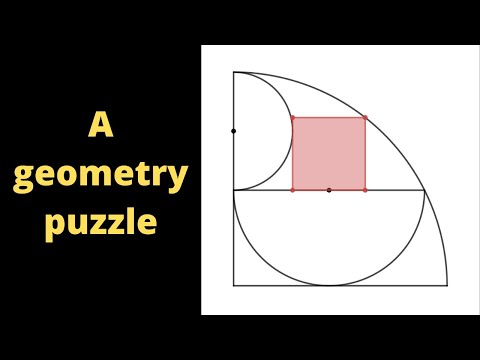
Unit square, a circle and two quarter circles (A geometry puzzle)
938. A semicircle and quarter circle inside a square. How long is the black tangent line?
Square Inscribed in a Semicircle
Комментарии
 0:03:08
0:03:08
 0:08:09
0:08:09
 0:06:20
0:06:20
 0:05:56
0:05:56
 0:08:58
0:08:58
 0:05:47
0:05:47
 0:07:22
0:07:22
 0:09:18
0:09:18
 0:56:16
0:56:16
 0:01:37
0:01:37
 0:01:15
0:01:15
 0:06:33
0:06:33
 0:13:24
0:13:24
 0:01:48
0:01:48
 0:06:33
0:06:33
 0:05:23
0:05:23
 0:00:44
0:00:44
 0:11:39
0:11:39
 0:08:58
0:08:58
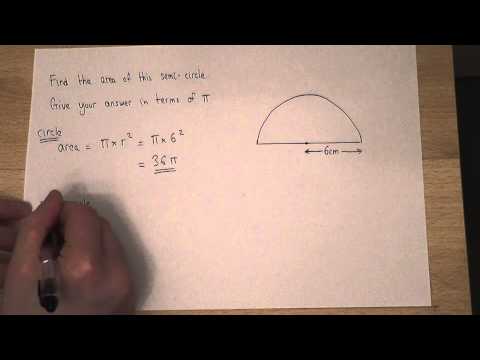 0:01:05
0:01:05
 0:09:04
0:09:04
 0:17:15
0:17:15
 0:00:54
0:00:54
 0:14:01
0:14:01