filmov
tv
Trigonometry - Finding the arc length of a circle

Показать описание
Arc Length of a Circle Formula - Sector Area, Examples, Radians, In Terms of Pi, Trigonometry
Trigonometry - Finding the arc length of a circle
Evaluating Inverse Trigonometric Functions (arcsin, arccos, arctan) Using Unit Circle
Finding arc length from radian angle measure | Trigonometry | Khan Academy
How to find the arc length of a circle using the formula
Radians and Degrees
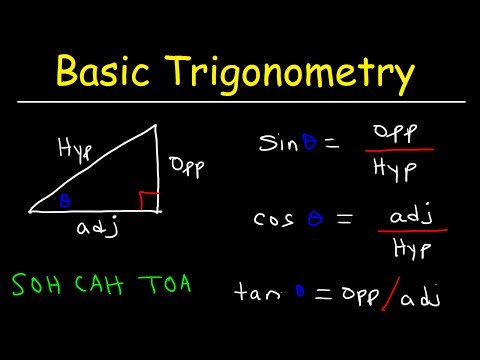
Trigonometry For Beginners!
Trigonometry: Arc Length & Area of a Sector (Section 3.4) | Math with Professor V
Finding Arc Length ❖ Trigonometry ❖ Pre-Calculus ❖ Geometry
Introduction to Trigonometry: Angles and Radians
🤯 This ONE CIRCLE will make you finally understand trigonometry #shorts
Example: Radian measure and arc length | Trigonometry | Khan Academy
Easy Way to Remember Derivatives of Trigonometry Ratios #shorts | How to Remember Derivatives Easily
Find the central angle given the arc length and radius
Find Arc Length Given Radius and Central Angle (2 Methods)
Six Trigs in 60 Seconds! #math #trigonometry
Trigonometry Concepts - Don't Memorize! Visualize!
All of TRIGONOMETRY in 36 minutes! (top 10 must knows)
Evaluating Inverse Trigonometric Functions
Learn to find the missing angles for a triangle using inverse trig functions
Sine vs Cosine: Who Will Win the Wave Race? #maths #trigonometry
Arc Length (Formula)
Trigonometry Basics : how to find missing sides and angles easily (6 Golden Rules of SOHCAHTOA)
HOW TO FIND ARC LENGTH AND SECTOR AREA OF CIRCLES | GEOMETRY
Комментарии
 0:15:57
0:15:57
 0:03:29
0:03:29
 0:08:56
0:08:56
 0:02:39
0:02:39
 0:02:14
0:02:14
 0:18:55
0:18:55
 0:21:52
0:21:52
 0:14:45
0:14:45
 0:02:42
0:02:42
 0:06:27
0:06:27
 0:01:00
0:01:00
 0:03:29
0:03:29
 0:00:50
0:00:50
 0:01:56
0:01:56
 0:02:15
0:02:15
 0:01:00
0:01:00
 0:32:35
0:32:35
 0:36:50
0:36:50
 0:22:47
0:22:47
 0:06:40
0:06:40
 0:00:17
0:00:17
 0:01:11
0:01:11
 0:07:24
0:07:24
 0:11:32
0:11:32