filmov
tv
1=0.999... using Cauchy sequences
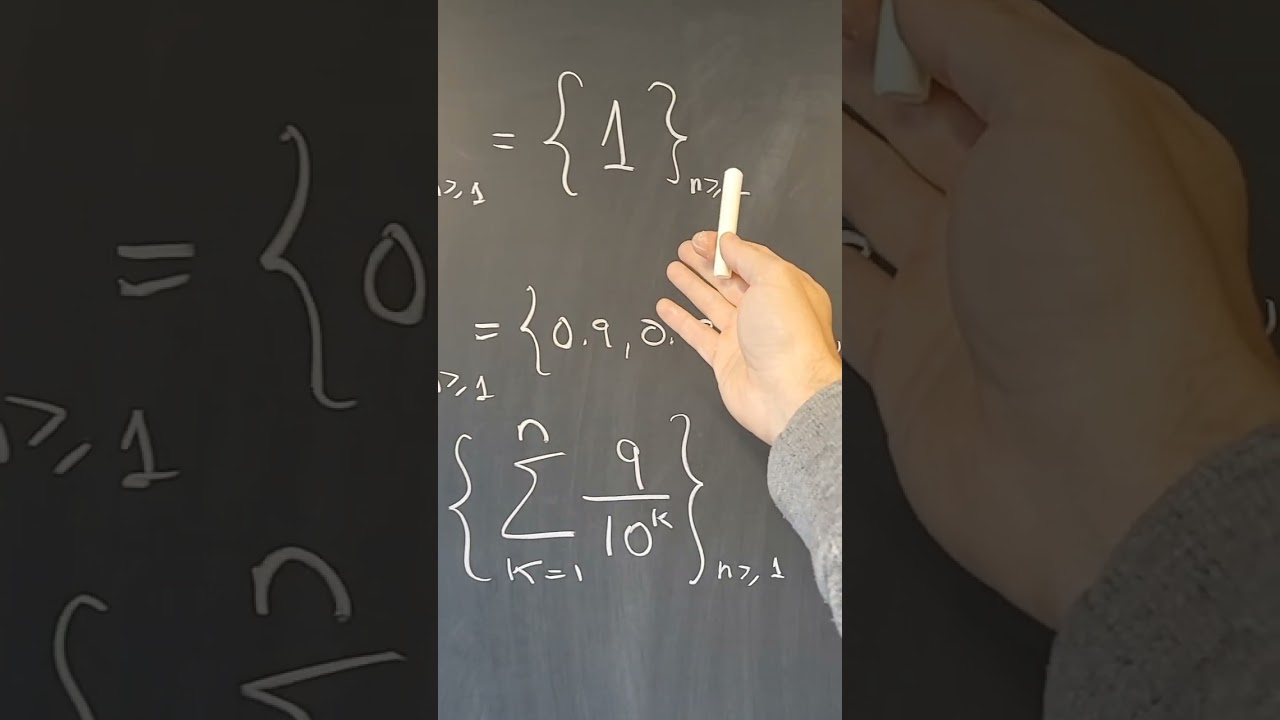
Показать описание
In this video I prove that 1=0.999... using the definition of the real numbers as equivalence classes of Cauchy sequences. #math #stem #cauchysequence #realnumbers #realanalysis
Proving 0.999...=1 [Real Analysis]
0 999... is not equal to 1 in this universe or any other
Proof of 0.9999…. = 1 using geometry series.
Cheating in exams😏!?
Why .999... = 1?
32 Metric Spaces-Cauchy Sequences. A Cauchy sequence need not be convergent in Metric Spaces
Incorrigible mainstream ignorance and stupidity: 1/3 = 0.333... implies 9 = 10.
A Sequence Problem that caused confusion in Cheenta
Are the real numbers... REAL?
0.999... does not equal 1 (Part 1: The Problem)
8 Digit length in rational numbers
Normed Space Important Theorm Every Convergent sequence in NORM SPACE is Cauchy Sequence Easy proof
Does 0.9999... = 1? NO : Why All Proofs for 0.999...=1 are Wrong. Please Discuss On Social Media
Intro to Real Analysis: How to think of real numbers
bcNotes 25 Testing for Divergence
0.999… Does Not Equal 1 : Intuitive Arguments For & Against (The Disbeliever, Part 2)
Cauchy General Principle of Convergence of a Sequence and one Problem by M. Arokiasamy
Limit of a Sequence with Examples | B.sc.2nd Year Math | ddu Gkp & SU | Part-5 @ASTEACH | AS Sir
Section 11.1. Sequences
proof 0.999...=1
Convergent sequence || convergence of sequence || Real analysis || Bsc maths
The 0.999...= 1 Controversy & Is Mathematics Fundamentally Flawed?
find a closed form for this INTIMIDATING SEQUENCE
Sequence | Wikipedia audio article
Комментарии
 0:10:49
0:10:49
 0:29:31
0:29:31
 0:03:49
0:03:49
 0:00:32
0:00:32
 0:33:51
0:33:51
 0:41:08
0:41:08
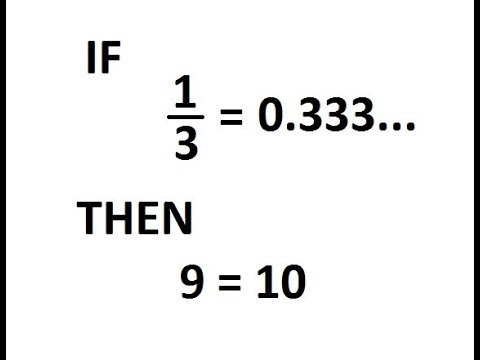 0:07:53
0:07:53
 0:10:00
0:10:00
 0:16:56
0:16:56
 0:08:16
0:08:16
 0:15:18
0:15:18
 0:09:21
0:09:21
 1:19:42
1:19:42
 0:18:15
0:18:15
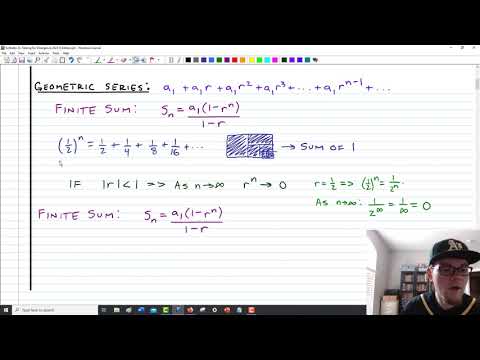 1:00:04
1:00:04
 0:11:50
0:11:50
 0:43:09
0:43:09
 0:45:47
0:45:47
 1:08:02
1:08:02
 0:10:20
0:10:20
 0:27:07
0:27:07
 0:21:37
0:21:37
 0:22:32
0:22:32
 1:12:39
1:12:39