filmov
tv
Cauchy General Principle of Convergence of a Sequence and one Problem by M. Arokiasamy

Показать описание
Cauchy's General Principle of Convergence of Sequence (Proof and examples) : 10
Cauchy general principle of convergence | Real Analysis | BSc | MSc
Cauchy general principal of convergence
Cauchy's General Principle of Convergence | Cauchy's Principles of Convergence |Real Analy...
Cauchy's General Principle of Convergence For Series | Infinite Series | Real Analysis | Lec-03
Sequence converges iff it is cauchy's sequence | cauchy's general principle of convergence
Problems based on Cauchy's General Principle of Convergence
Using Cauchy's General Principle of Convergence, sequence is not Convergent.
Cauchy's General Principle of Convergence of Sequence | Question | Real Analysis | MA CLASSES
Real Analysis | Cauchy Sequence | Cauchy Sequence Example & Definition
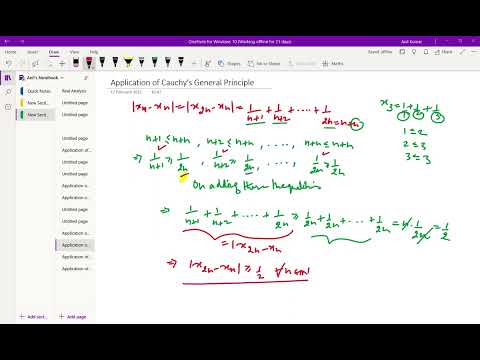
Application of Cauchy's General Principle of Convergence
Cauchy's general principle of convergence of a sequence
Cauchy general principle of convergence Example.
Cauchy's General Principle of Convergence
Cauchy General Principles of Convergence Proof | Sequence and Series | Real Analysis | Bsc maths
Cauchy's general principle of convergence of sequence | Proof and practice | real sequences 10 ...
Cauchy's general principle of convergence
#40 Cauchy general principle of convergence of series | Infinite series with positive and negative
Cauchy's General Principle of Convergence ( Sequences and series)
Cauchy General Principle of Convergence | Real Analysis Lecture 22 | BS / MSc Mathematics Lectures
Problems on Cauchy's General Principle of convergence of a series: M. Arokiasamy
Real analysis | cauchy's general principle of convergence for series | theorem proof | series
Apply Cauchy's general principle of convergence prove 1- 1/2+ ... +(-1)^(n-1)/n.... is conver...
Cauchy General Principle of Convergence of a Sequence and one Problem by M. Arokiasamy
Комментарии
 0:46:14
0:46:14
 0:07:43
0:07:43
 0:10:15
0:10:15
 0:13:44
0:13:44
 0:20:44
0:20:44
 0:18:58
0:18:58
 0:26:38
0:26:38
 0:17:32
0:17:32
 0:23:09
0:23:09
 0:15:01
0:15:01
 0:23:22
0:23:22
 0:06:49
0:06:49
 0:08:13
0:08:13
 0:17:54
0:17:54
 0:14:14
0:14:14
 0:34:05
0:34:05
 0:20:15
0:20:15
 0:15:57
0:15:57
 0:07:37
0:07:37
 0:09:45
0:09:45
 0:21:41
0:21:41
 0:16:54
0:16:54
 0:09:22
0:09:22