filmov
tv
Integral of 1/(x^2+1) from -inf to inf, Contour Integral

Показать описание
BIG SHOUT OUT TO THE SUPERFAN, CHESTER, who subscribed to my channel when I had less then 1k subs!!!!!!
In this freestyle, right on the spot lecture, Dr. Peyam explains how to integrate 1/(x^2+1) from -inf to inf by using contour integration from complex analysis. This is a great starter for the people who are interested in this topic!
My Game Changers!
Check out my site & social media
blackpenredpen
100/(1-x)
In this freestyle, right on the spot lecture, Dr. Peyam explains how to integrate 1/(x^2+1) from -inf to inf by using contour integration from complex analysis. This is a great starter for the people who are interested in this topic!
My Game Changers!
Check out my site & social media
blackpenredpen
100/(1-x)
Integral of 1/(x^2+1) from -inf to inf, Contour Integral
Integral of 1/(1 + x^2) from 0 to infinity
The Improper Integral of 1/(x^2 + 1) from 0 to infinity
Comparison Theorem doesn't work, integral of 1/(x^2-1), calculus 2 tutorial
integral of dx / 1 + x² from negatif infinity to infinity
integral of 1/(x^2+1) but you didn't learn it this way in calculus 2
integral of 2/(x^2-1) from 1 to inf (both type 1 and type 2)
Improper Integral of 1/(1+x^2) from Negative Infinity to Positive Infinity (-inf to +inf)
Ramblings from Calculus 1 before Exam 3 (Fall 2024)
Improper integral of 1/x^2 from 1 to infinity.
Evaluate Improper Integral 1/(x^2 + x) dx over [1, infinity). Infinite Integration Limits
Integral of 1/x from 1 to Infinity
Improper Integral of 1/x^2 from 2 to infinity
Integral of 1/x
Improper Integral: 1/x^2 evaluated from 0 to 1
Integral 1/x^2 + 1 two ways
Type 1 improper integrals! calculus 2
Integral 1/1-x^2 two ways
You're gonna love this satisfying integration problem (integral from zero to infinity of 1/(x^4...
The p-integral Proof (type 1 improper integral)
How REAL Men Integrate Functions
Improper Integrals - Convergence and Divergence - Calculus 2
complex contour example: ln(1+x^2)/(1+x^2) from 0 to infinity
Every Student Should See This
Комментарии
 0:19:50
0:19:50
 0:03:22
0:03:22
 0:02:49
0:02:49
 0:15:14
0:15:14
 0:03:04
0:03:04
 0:09:21
0:09:21
 0:11:46
0:11:46
 0:13:14
0:13:14
 0:41:06
0:41:06
 0:02:59
0:02:59
 0:04:41
0:04:41
 0:01:34
0:01:34
 0:03:21
0:03:21
 0:00:50
0:00:50
 0:06:15
0:06:15
 0:14:41
0:14:41
 0:27:48
0:27:48
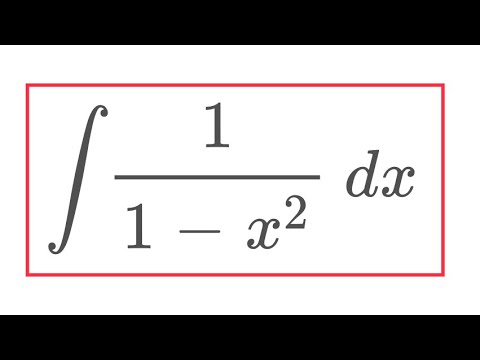 0:12:32
0:12:32
 0:08:33
0:08:33
 0:08:31
0:08:31
 0:00:35
0:00:35
 0:13:56
0:13:56
 0:07:43
0:07:43
 0:00:58
0:00:58