filmov
tv
A complex number z is said to be unimodular if . Suppose `z_1` and `z_2` are complex numbers...
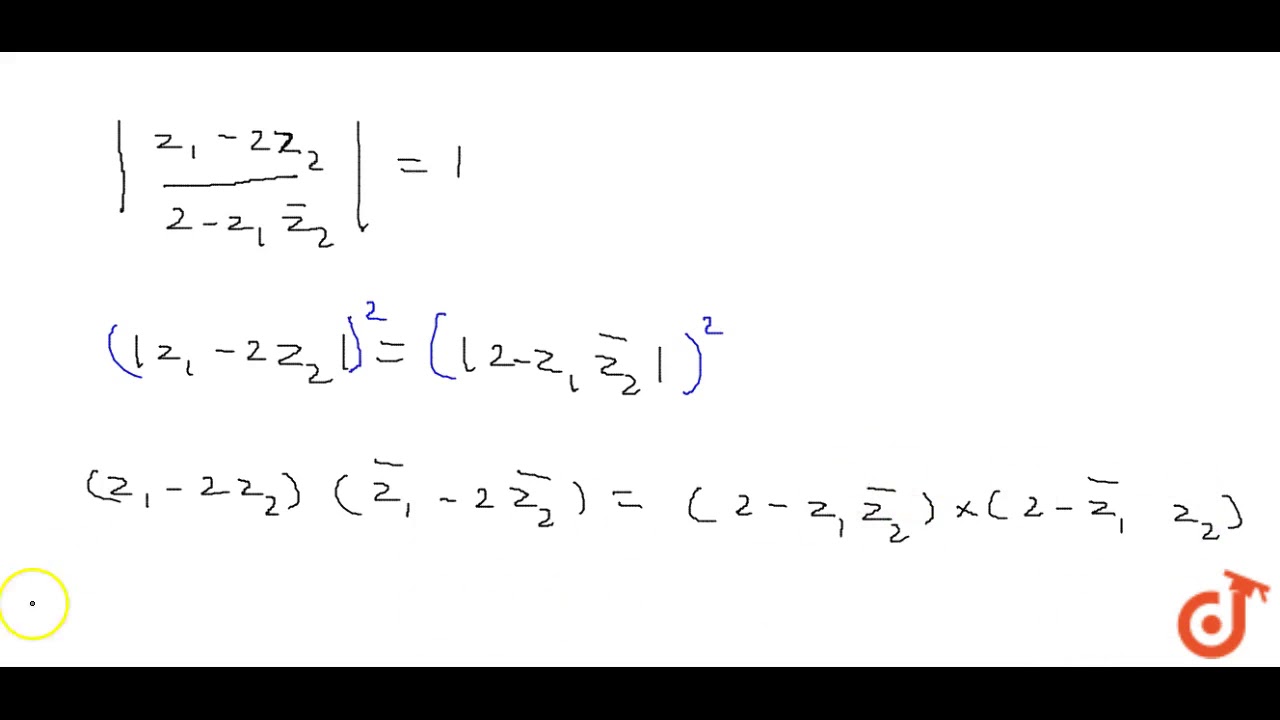
Показать описание
complex number z is said to be unimodular if . Suppose `z_1`
and `z_2`
are complex numbers such that `(z_1-2z_2)/(2-z_1z_2)`
is unimodular and `z_2`
is not unimodular. Then the point `z_1`
lies
on a :
(1)
straight line parallel to x-axis
(2) straight line parallel to y-axis
(3)
circle of radius 2
(4) circle of radius `sqrt(2)`
and `z_2`
are complex numbers such that `(z_1-2z_2)/(2-z_1z_2)`
is unimodular and `z_2`
is not unimodular. Then the point `z_1`
lies
on a :
(1)
straight line parallel to x-axis
(2) straight line parallel to y-axis
(3)
circle of radius 2
(4) circle of radius `sqrt(2)`
![Expressing Real Re[z]](https://i.ytimg.com/vi/qiz5U3ktnQM/hqdefault.jpg) 0:10:54
0:10:54
 0:07:39
0:07:39
 0:08:04
0:08:04
 0:02:35
0:02:35
 1:04:47
1:04:47
 0:16:50
0:16:50
 0:05:39
0:05:39
 0:03:00
0:03:00
 1:11:16
1:11:16
 0:02:34
0:02:34
 0:10:26
0:10:26
 0:03:55
0:03:55
 0:09:03
0:09:03
 0:06:33
0:06:33
 0:02:20
0:02:20
 0:04:43
0:04:43
 0:01:55
0:01:55
 0:19:52
0:19:52
 0:10:46
0:10:46
 0:06:46
0:06:46
 0:03:56
0:03:56
 0:02:07
0:02:07
 0:06:18
0:06:18
 0:40:02
0:40:02