filmov
tv
graphing |z-1|=2 , in the complex plane (related videos in desc. below)
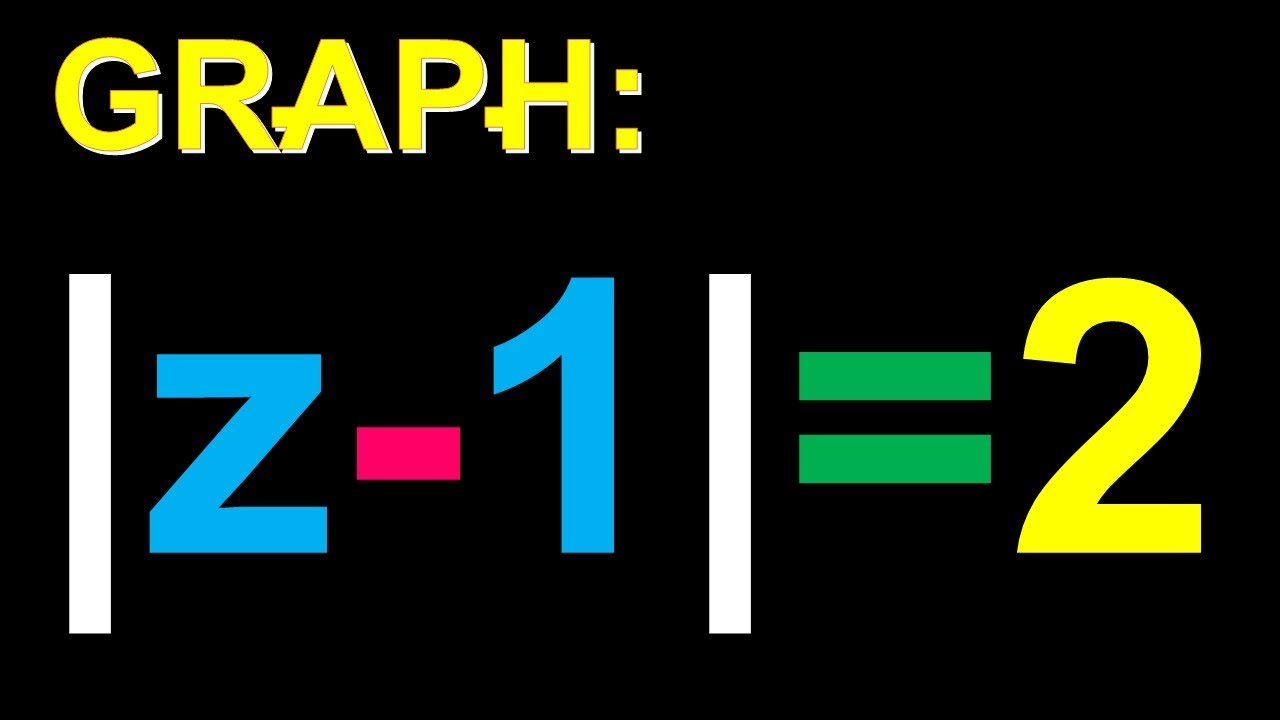
Показать описание
We start with the equation |z - 1| = 2, where z is a complex number.
Let z = x + yi, where x and y are real numbers. Substituting this into the equation, we get:
|(x + yi) - 1| = 2
Simplifying the left-hand side, we have:
√((x - 1)² + y²) = 2
Squaring both sides of the equation, we get:
(x - 1)² + y² = 4
This is the equation of a circle with center (1,0) and radius 2. To see this, we can use the standard form equation for a circle:
(x - h)² + (y - k)² = r²
where (h,k) is the center of the circle and r is the radius. Comparing this with the equation we obtained, we see that h = 1, k = 0, and r = 2, which gives us the equation:
(x - 1)² + y² = 2²
To graph the circle on the x-y plane, we plot the center point (1,0) and then draw a circle with radius 2 around it. This gives us the graph of the equation |z - 1| = 2 in the Cartesian plane, which is a circle with center (1,0) and radius 2.
---------------------------------------------------------------------------------------------------------------------------------------------------------
Here's how we can graph the equation |z - 1| = 1, where z is a complex number:
Let z = x + yi, where x and y are real numbers. Substituting this into the equation, we get:
|(x + yi) - 1| = 1
Simplifying the left-hand side, we have:
√((x - 1)² + y²) = 1
Squaring both sides of the equation, we get:
(x - 1)² + y² = 1
This is the equation of a circle with center (1,0) and radius 1. To see this, we can use the standard form equation for a circle:
(x - h)² + (y - k)² = r²
where (h,k) is the center of the circle and r is the radius. Comparing this with the equation we obtained, we see that h = 1, k = 0, and r = 1, which gives us the equation:
(x - 1)² + y² = 1²
To graph the circle on the x-y plane, we plot the center point (1,0) and then draw a circle with radius 1 around it. This gives us the graph of the equation |z - 1| = 1 in the Cartesian plane, which is a circle with center (1,0) and radius 1.
----------------------------------------------------------------------------------------------------------------------------------------------------------
Here's how we can graph the equation |z + 1| = 2, where z is a complex number:
Let z = x + yi, where x and y are real numbers. Substituting this into the equation, we get:
|(x + yi) + 1| = 2
Simplifying the left-hand side, we have:
√((x + 1)² + y²) = 2
Squaring both sides of the equation, we get:
(x + 1)² + y² = 4
This is the equation of a circle with center (-1,0) and radius 2. To see this, we can use the standard form equation for a circle:
(x - h)² + (y - k)² = r²
where (h,k) is the center of the circle and r is the radius. Comparing this with the equation we obtained, we see that h = -1, k = 0, and r = 2, which gives us the equation:
(x + 1)² + y² = 2²
To graph the circle on the x-y plane, we plot the center point (-1,0) and then draw a circle with radius 2 around it. This gives us the graph of the equation |z + 1| = 2 in the Cartesian plane, which is a circle with center (-1,0) and radius 2.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
Let z = x + yi, where x and y are real numbers. Substituting this into the equation, we get:
|(x + yi) - 1| = 2
Simplifying the left-hand side, we have:
√((x - 1)² + y²) = 2
Squaring both sides of the equation, we get:
(x - 1)² + y² = 4
This is the equation of a circle with center (1,0) and radius 2. To see this, we can use the standard form equation for a circle:
(x - h)² + (y - k)² = r²
where (h,k) is the center of the circle and r is the radius. Comparing this with the equation we obtained, we see that h = 1, k = 0, and r = 2, which gives us the equation:
(x - 1)² + y² = 2²
To graph the circle on the x-y plane, we plot the center point (1,0) and then draw a circle with radius 2 around it. This gives us the graph of the equation |z - 1| = 2 in the Cartesian plane, which is a circle with center (1,0) and radius 2.
---------------------------------------------------------------------------------------------------------------------------------------------------------
Here's how we can graph the equation |z - 1| = 1, where z is a complex number:
Let z = x + yi, where x and y are real numbers. Substituting this into the equation, we get:
|(x + yi) - 1| = 1
Simplifying the left-hand side, we have:
√((x - 1)² + y²) = 1
Squaring both sides of the equation, we get:
(x - 1)² + y² = 1
This is the equation of a circle with center (1,0) and radius 1. To see this, we can use the standard form equation for a circle:
(x - h)² + (y - k)² = r²
where (h,k) is the center of the circle and r is the radius. Comparing this with the equation we obtained, we see that h = 1, k = 0, and r = 1, which gives us the equation:
(x - 1)² + y² = 1²
To graph the circle on the x-y plane, we plot the center point (1,0) and then draw a circle with radius 1 around it. This gives us the graph of the equation |z - 1| = 1 in the Cartesian plane, which is a circle with center (1,0) and radius 1.
----------------------------------------------------------------------------------------------------------------------------------------------------------
Here's how we can graph the equation |z + 1| = 2, where z is a complex number:
Let z = x + yi, where x and y are real numbers. Substituting this into the equation, we get:
|(x + yi) + 1| = 2
Simplifying the left-hand side, we have:
√((x + 1)² + y²) = 2
Squaring both sides of the equation, we get:
(x + 1)² + y² = 4
This is the equation of a circle with center (-1,0) and radius 2. To see this, we can use the standard form equation for a circle:
(x - h)² + (y - k)² = r²
where (h,k) is the center of the circle and r is the radius. Comparing this with the equation we obtained, we see that h = -1, k = 0, and r = 2, which gives us the equation:
(x + 1)² + y² = 2²
To graph the circle on the x-y plane, we plot the center point (-1,0) and then draw a circle with radius 2 around it. This gives us the graph of the equation |z + 1| = 2 in the Cartesian plane, which is a circle with center (-1,0) and radius 2.
Please visit our Merch Stores and help support the spreading of knowledge:)
Our T-Shirt Merch:
Our Amazon Store for Awesome Merch too:
Комментарии
 0:04:43
0:04:43
 0:08:05
0:08:05
 0:01:51
0:01:51
 0:04:18
0:04:18
 0:05:15
0:05:15
 0:00:15
0:00:15
 0:11:18
0:11:18
 0:14:52
0:14:52
 0:05:47
0:05:47
 0:04:55
0:04:55
 0:43:11
0:43:11
 0:10:04
0:10:04
 0:09:22
0:09:22
 0:00:17
0:00:17
 0:05:36
0:05:36
 0:07:27
0:07:27
 0:07:06
0:07:06
 0:15:28
0:15:28
 0:11:07
0:11:07
 0:10:52
0:10:52
 0:07:28
0:07:28
 0:03:49
0:03:49
 0:08:46
0:08:46
 0:07:48
0:07:48